Después de haber visto distintos tipos de amplificadores que se pueden construir usando Amplificadores Operacionales, en este capítulo describiremos dos circuitos clásicos que representan a las operaciones matemáticas de suma y resta, y que son llamados apropiadamente Sumador y Restador.
También presentamos un circuito de aplicación práctica correspondiente a un mezclador de audio completo y que puede ser usado como parte de un sistema de sonido.
12.1 Amplificador Sumador
Teniendo en mente que un OPAMP realimentado negativamente, y en equilibrio, tratará de mantenerse en equilibrio inyectando una corriente por la red de realimentación que va a la entrada inversora (el principio de funcionamiento del amplificador inversor), podemos intuir que un amplificador sumador se puede construir a partir de un amplificador inversor, como el mostrado en la siguiente figura:
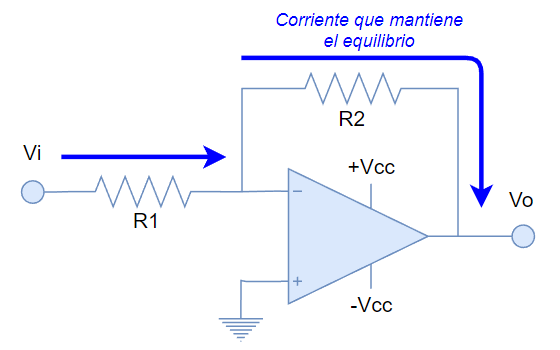
El amplificador inversor es un buen punto de partida para diseñar un amplificador sumador porque la entrada inversora de esta configuración es una tierra virtual, y toda corriente que ingrese (o salga) por R1, hacia esa tierra virtual, es susceptible de ser medida, porque esa misma corriente se convierte en voltaje por efecto de R2.
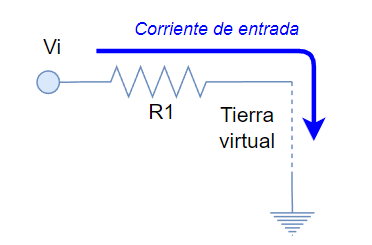
En resumen esa es la explicación de funcionamiento del amplificador inversor, y basándonos en ese único razonamiento, pudimos haber deducido que el voltaje de salida es: -(R2/R1) * Vi
Ahora, lo particular de esta configuración es que realmente convertimos corriente a voltaje. La corriente a convertir a voltaje es la que entra por R1 hacia la tierra virtual, de modo que, da lo mismo si esa corriente llega a través de una resistencia o de varias.
Entonces, para sumar voltajes, bastaría convertir esos voltajes a corrientes y aplicarlas a la tierra virtual, de modo que se sumen las corrientes también. La configuración final de sumador, para dos entradas, sería la que se muestra en la figura:
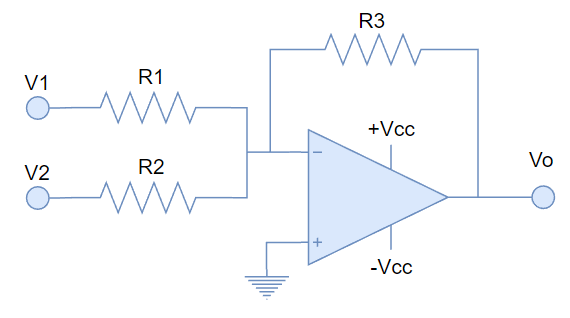
Con el análisis anterior, podemos deducir que la corriente que va a la tierra virtual es la suma de las corrientes que ingresan por las dos entradas:
I_o = \frac{V1}{R1} + \frac{V2}{R2}Luego, podemos calcular el voltaje de salida que el OPAMP fijará para mantener el equilibrio de la realimentación:
V_o = -I_o.R3
Uniendo estas dos ecuaciones tendremos la función de salida:
V_o = -(\frac{R3}{R1}.V1 + \frac{R3}{R2}.V2)En la forma actual, este amplificador obtiene lo que sería una suma ponderada del voltaje de las entradas. Para simplificar la ecuación, nos conviene hacer que las resistencias de entrada sean iguales (R1 = R2 = R). Y si ahora llamamos Ra a la resistencia de realimentación, tendríamos el siguiente circuito:
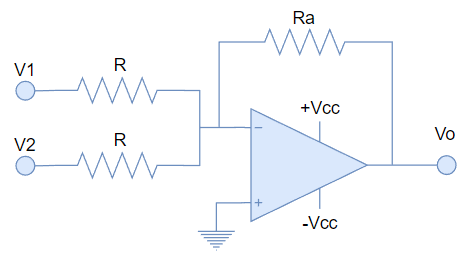
Que tiene la siguiente fórmula de salida:
V_o = -\frac{Ra}{R}.(V1 + V2)Lo que tiene ya la forma de amplificador sumador, porque suma los voltajes de entrada. Se puede deducir que podemos agregar más entradas, agregando una resistencia más por cada entrada adicional.
La impedancia de entrada, de cada entrada, es igual a R. Esto se puede deducir de forma sencilla teniendo en mente que la entrada inversora está unida virtualmente a tierra.
Con este amplificador tenemos, además, la ventaja de que podemos conseguir una ganancia que sería equivalente a -Ra/R, que invierte la polaridad de la suma porque estamos trabajando sobre un diseño de Amplificador inversor, así que, lo que realmente tenemos es un «Amplificador Sumador Inversor».
Si se desea corregir la polaridad de la salida, solo bastaría con colocar un amplificador inversor de ganancia -1 a la salida de este amplificador.
12.2 Sumador no inversor
También podemos implementar una configuración de amplificador sumador no inversor, como se muestra en la siguiente figura:
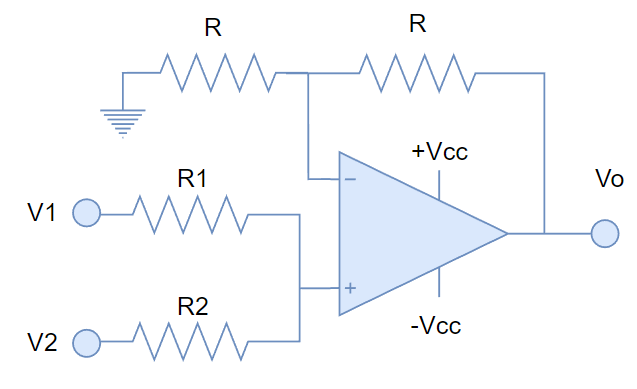
Para analizar este circuito, llamemos Vi al voltaje de la entrada no inversora, y analizando por mallas podemos llegar a la siguiente fórmula:
\begin{align}
Vi = (V1-V2).\frac{R2}{R1+R2} + V2
\end{align} Por otro lado, la salida la podemos expresar como:
\begin{align}
Vo = 2.Vi
\end{align} Por lo tanto, la función de salida será:
Vo = 2(V1-V2).\frac{R2}{R1+R2} + V2Simplificando, obtenemos:
\begin{align}
Vo = 2\frac{R2}{R1+R2}V1+ 2\frac{R1}{R1+R2}V2
\end{align} Esta configuración, nos da, a la salida, una suma ponderada del voltaje de las entradas. Si hacemos R1 = R2 = Re, tendremos el siguiente circuito:
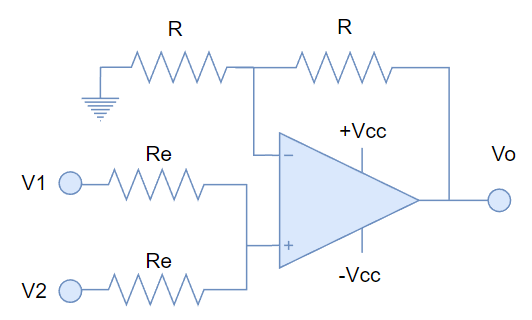
Con la siguiente función de salida:
Vo = V1+ V2
Que sería la forma más compacta de un amplificador sumador, con la ventaja de que no se necesita corregir la polaridad de la salida. Sin embargo, y en comparación con el amplificador sumador inversor, este circuito:
- Requiere de una resistencia adicional.
- La impedancia de entrada, en una entrada cualquiera, es afectada por la impedancia de salida de la otra entrada.
- La precisión del voltaje de salida depende de más parámetros (más resistencias).
- Requiere de una análisis más complejo.
Por estos motivos, esta configuración no suele usarse mucho, salvo en casos en que sea importante mantener la polaridad de la suma con pocos componentes.
En particular, la dificultad para fijar la impedancia de entrada, es lo que hace poco agradable a este circuito. Un rápido análisis visual del circuito, nos revelará que si quisiéramos tener un valor alto de impedancia de entrada, debemos usar valores altos de Re. De esta forma también reduciremos la interdependencia que tenemos entre las entradas. Pero no olvidar que, los puntos de un circuito con impedancia alta son fuentes sensibles de interferencia estática.
Una aplicación directa directa de los sumadores sería en la implementación de computadoras analógicas, pero también se pueden usar en mezcladores de audio, porque la mezcla de sonido es, matemáticamente, una suma de los voltajes de las líneas de audio.
12.3 Restador
La implementación de un circuito restador la podemos hacer directamente a partir de la configuración de amplificador diferencial que vimos en el Capítulo 11, y que se muestra a continuación:

Sabemos que en este circuito la función de salida es:
V_o = \frac{R2}{R1} (V_2 - V_1)
Que tiene ya la forma de un amplificador restador con un nivel de amplificación o atenuación que se puede conseguir variando R2 y R1.
Si quisiéramos un restador exacto, deberíamos hacer R1 y R2, con lo que obtenemos:
V_o = (V_2 - V_1)
Como esta función es independiente de los valores de R1 y R2, eso nos deja libertad para ajustar estas resistencias y así controlar la impedancia de entrada.
A primera vista, la impedancia de entrada de cada entrada, con respecto a tierra debe ser mayor que R1. Si quisiéramos un análisis más detallado de la impedancia de entrada en modo común, podemos unir las dos entradas y analizar la corriente de entrada:
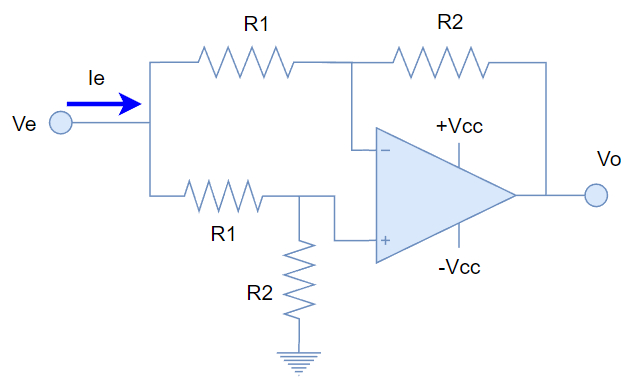
Para este análisis, consideramos las dos ramas de entrada que se comportarán como resistencias en paralelo.
La rama de la entrada inversora, tiene una impedancia de entrada de R1+R2, porque estamos despreciando la impedancia de entrada del propio OPAMP.
\begin{align}
Rcm1 = R1 + R2
\end{align} Para analizar la rama de la entrada no inversora, nos conviene considerar el corto circuito virtual que existe entre las entradas del OPAMP:
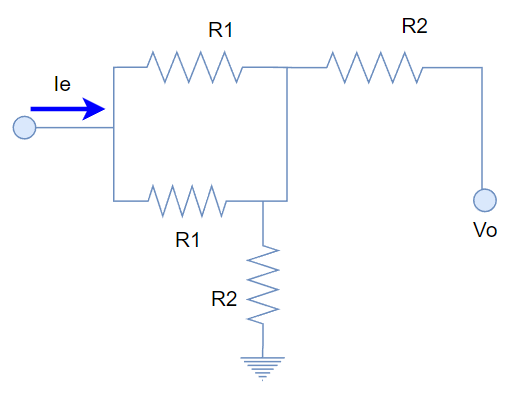
Como podemos asumir que la salida tiene impedancia cero, la resistencia equivalente que vemos desde esa rama sería:
\begin{align}
Rcm2 = \frac{R1 + R2}{2}
\end{align} Juntando (4) y (5), que, se encuentran en paralelo, llegaremos al valor de la impedancia de entrada en modo común:
\begin{align}
Rcm = \frac{R1 + R2}{3}
\end{align} La impedancia de entrada en modo diferencial se puede calcular siguiendo el mismo razonamiento, y , como la conexión virtual entre las entradas inversora y no inversora solo va en un sentido, obtendremos que la impedancia entre las entradas sería equivalente a la de las dos ramas en serie:
\begin{align}
Rdm = \frac{3}{2}(R1+R2)
\end{align} Hay que notar, sin embargo, que la corriente de entrada pasa primero por tierra, cuando analizamos el caso diferencial.
Al igual que los circuitos sumadores, los circuitos restadores son útiles en la construcción de computadoras analógicas, pero también se pueden usar en cualquier fase del procesamiento de señales analógicas en donde se requiera realizar una resta de voltajes.
12.4 Caso Práctico: Mezclador de audio
Como ejemplo aplicativo, del uso de circuitos sumadores, pasemos a implementar un mezclador de audio.
En principio, y sin mucha complicación, podríamos pensar en implementar un mezclador pasivo, en la forma de un par de resistencias:
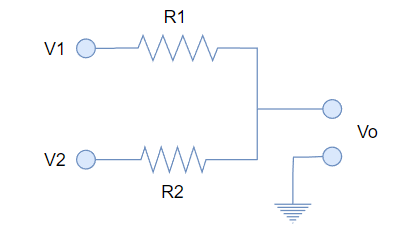
Este circuito, aunque funcional, tiene algunas desventajas:
- Existe interconexión entre la entradas (como en el caso del Amplificador sumador no inversor), por lo que no se puede controlar la impedancia de cada entrada, independientemente de la otra.
- Existe interconexión entre la entrada y la salida, por lo que también la salida conectada, afectará a la impedancia de entrada.
- La impedancia de salida se ve afectada por las impedancias de salida de cada una de las entradas.
- La salida nunca llegará a obtener la suma efectiva de voltajes, porque siempre existirá una atenuación que, en el mejor de los casos, será de 1/2 (Ver ecuación 1).
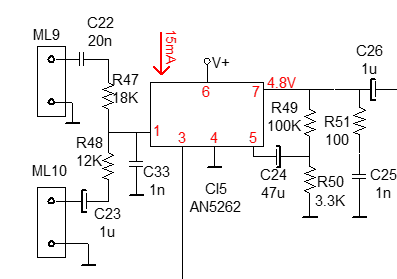
A pesar de estas desventajas, puede haber situaciones en las que basta con esta configuración de mezclador pasivo. El siguiente circuito pertenece a un circuito comercial de un sistema de audio:

El mezclador pasivo lo componen R47 y R48, que inyectan la señal a la entrada del CI AN5262. Las entradas están conectadas a otra tarjeta del circuito, de modo que el efecto de estas impedancias de salida, que son fijas y conocidas, se han considerado en el diseño.
Un diseño más tolerable a las impedancias de entrada y con mejor posibilidad de controlar la ganancia, se puede lograr con el uso de Amplificadores Operacionales.
Para ello partimos del circuito del clásico sumador que ya hemos visto, pero complementándolo con los componentes necesarios que se requieren para el manejo de audio.
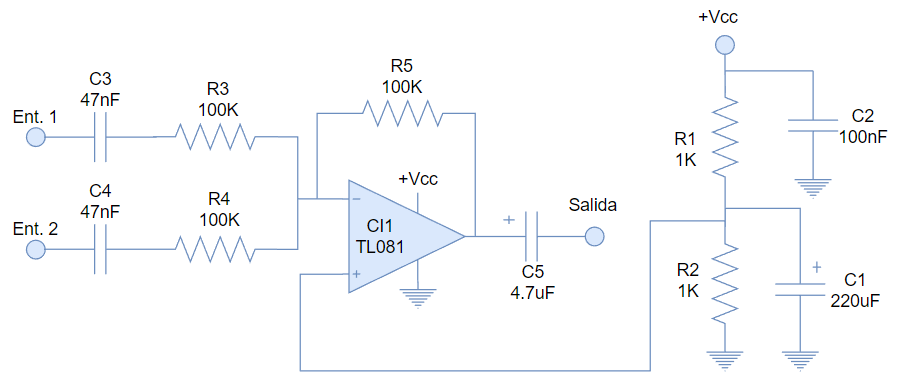
Este circuito se ha creado a partir del diseño de preamplificador de audio mostrado en la sección 10.6, al que se le ha añadido una entrada adicional y se le ha reducido la ganancia.
La conveniencia del uso de un amplificador inversor para un preamplificador de audio, se detalló en la sección 10.6 y sigue siendo válido para el caso de este mezclador.
La impedancia de cada entrada es 100K y está determinada por las resistencias R3 y R4. Es posible agregar entradas adicionales sin problema, conectando una nueva entrada con su resistencia y condensador respectivo.
La ganancia del mezclador es unitaria porque solo deseamos implementar una suma de las señales de entrada sin amplificación, como es común en un mezclador de audio.
El rango dinámico de entrada puede variar desde -5V a +5V aproximadamente (10Vpp o 10V de pico a pico), si alimentamos al circuito con 12V. Ese valor se puede deducir notando que el valor del voltaje de salida es igual al voltaje de entrada pero invertido, de modo que, como el voltaje de salida para este OPAMP lo fijamos en el rango de +1V a +Vcc – 1V, también la entrada debe estar dentro de ese rango (pero referenciada a tierra). Un detalle importante es notar que cuando decimos que el rango dinámico de la entrada es de 10Vpp, nos referimos a la suma de las entradas. Así, por ejemplo, si la entrada 1 tiene un valor de 5Vpp y la entrada 2 de 5Vpp, ya estarían en el límite del rango de entrada, si las entradas están en fase.
Como en la cadena de audio, manejamos niveles de 1Vpp, no tendremos problemas con nuestro mezclador, pero hay que considerar que dos entradas de 1Vpp, pueden producir una salida de 2Vpp. El problema es mayor si tenemos más entradas.
Este circuito se diseñó para trabajar a 12V pero se puede reducir sin problemas hasta 10V o 9V (reduciendo el rango dinámico de las entradas). Se puede conectar directamente a una batería, o a una fuente de alimentación. En este último caso, conviene incluir una red de filtrado adicional, antes de alimentar al mezclador.
El detalle de los condensadores a las entradas, es para desacoplar la componente DC que puedan aparecer a las entradas, porque la señal de audio es de tipo AC, pero nada garantiza que pueda venir con algún nivel de DC. Los valores de C3 y C4 constituyen filtro pasa altos en cada entrada, con ayuda de las resistencias R3 y R4. Más adelante se dará más información sobre los filtros implementados con OPAMP.
En este diseño no se han incluido potenciómetros de entrada porque como circuito mezclador, no se espera que tenga algún nivel de amplificación variable. De ser necesario, no habría ningún inconveniente en incluir potenciómetros para regular el nivel de cada entrada y también se podría incluir un nivel de ganancia adicional en el circuito.
12.5 Ejercicios
EJERCICIO 1. ¿Por qué se prefiere usar amplificadores sumadores inversores? ¿Cuál sería la desventaja?
EJERCICIO 2. ¿Cómo mejorar la impedancia de entrada de un amplificador restador de ganancia unitaria?
EJERCICIO 3. ¿Cuál es la diferencia entre un amplificador diferencial y un amplificador restador?
EJERCICIO 4. ¿Cómo convertir corriente a voltaje en un circuito con OPAMP?
EJERCICIO 5. Hallar la función de salida del siguiente circuito:
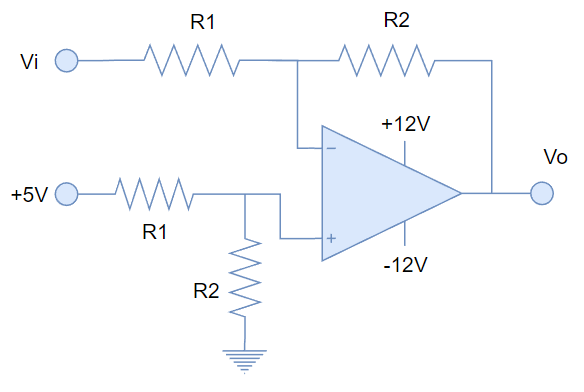
![]() ¿Cómo citar este artículo?
¿Cómo citar este artículo?
- En APA: Hinostroza, T. (22 de junio de 2024). OPAMP – Cap. 12 – Sumadores y Restadores. Blog de Tito. https://blogdetito.com/2024/06/22/opamp-cap-12-sumadores-y-restadores/
- En IEEE: T. Hinostroza. (2024, junio 22). OPAMP – Cap. 12 – Sumadores y Restadores. Blog de Tito. [Online]. Available: https://blogdetito.com/2024/06/22/opamp-cap-12-sumadores-y-restadores/
- En ICONTEC: HINOSTROZA, TIto. OPAMP – Cap. 12 – Sumadores y Restadores [blog]. Blog de Tito. Lima Perú. 22 de junio de 2024. Disponible en: https://blogdetito.com/2024/06/22/opamp-cap-12-sumadores-y-restadores/

Dejar una contestacion