10.1 Introducción
En el capítulo anterior vimos cómo implementar el reconocimiento de las variables de nuestro compilador, usando la sintaxis de nuestro lenguaje Titan.
En este artículo, veremos cómo podemos implementar una rutina para la carga de operandos en la CPU o en la RAM. Pero para ello, necesitamos primeramente manejar algunos conceptos teóricos importantes.
10.2 Teoría de Compiladores
Las expresiones
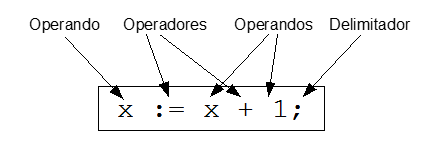
Entendemos como expresiones al conjunto de operandos y operadores, como en el siguiente ejemplo:
1 + 2
En este ejemplo, los números 1 y 2 constituyen los operandos, mientras que el símbolo «+» es el operador.
Las expresiones pueden ser más complejas que una simple suma:
x + y * (1+abs(j) )
Probablemente las expresiones sean los elementos más abundantes en la mayoría de los lenguajes de programación.
Notación de las expresiones
Las expresiones se pueden expresar en diversas notaciones:
- Notación Infijo: 1 + 2 * 3
- Notación Prefijo: * 2 3 + 1
- Notación Postfijo: 2 3 * 1 +
Las expresiones más comunes son las de tipo Infijo, porque se asemejan a la forma en que se expresan las expresiones que nos enseñaron en el colegio.
Las otras formas son poco comunes y se usan en algunos tipos de calculadoras (como algunos modelos de HP) o lenguajes (como el Forth).
En nuestro compilador trataremos las expresiones en notación Infijo.
Operadores
Los operadores, conjuntamente con los operandos, conforman las expresiones. Los operadores determinan las operaciones que deben realizarse dentro de una expresión.
Si analizamos los operadores en las expresiones en Infijo, como en el siguiente ejemplo:
a + b + c
Y tratamos de resolverla, empezaríamos evaluando primero a + b, luego ese resultado lo evaluaremos con c.
En este proceso, podemos notar que los operadores se aplican siempre a dos operandos.
A este tipo de operadores les llamaremos Operadores binarios. La mayoría de los operadores caen en esta categoría, como la suma (+), resta (-) o multiplicación (*).
Pero también existen operadores que se aplican a un solo operando, como el operador de incremento de C (++) o el de decremento (–). A este tipo de operadores se les llama Operadores Unarios.
Precedencia de operadores
Las expresiones se evalúan siempre aplicando la operación, que define el operador, sobre los operandos, para luego usar el resultado como un nuevo operador para aplicar el siguiente operador, si es que existiese.
En una expresión sencilla que solo use un solo tipo de operador, la evaluación se suele hacer en la forma en que se lee la expresión, de izquierda a derecha. Así si la expresión es:
a + b + c + d
El orden de evaluación será:
((a + b) + c) + d
Sin embargo, se puede asignar mayor prioridad a algunos operadores sobre otros para forzar a que se evalúen antes. A esta prioridad se le llama «Precedencia» y determina el orden de evaluación de las expresiones. Como ejemplo consideremos el caso en que le asignamos mayor precedencia al operador de multiplicación (*) que al de suma (+), entonces la expresión:
a + b * c
Se deberá evaluar como:
a + (b * c)
La precedencia de operadores está bien definida en los lenguajes de programación, aunque cada lenguaje puede definir un esquema de precedencia distinto.
10.3 Lectura de operandos
La primera parte en la implementación de un verdadero analizador de expresiones es el reconocimiento de operandos.
Como nuestro compilador es de una sola pasada y con contamos con un AST, nuestra lectura de operandos debe estar complementada con la generación del código necesario para la lectura de esos operandos.
Como se explicará en la sección 12, los analizadores de expresiones pueden estar orientados a pila o a registro. En nuestro caso, optaremos por orientarnos a registros, así que nuestra rutina de lectura de operandos dejará el valor de todos los operandos dentro de registros predeterminados de la CPU [1. Pudimos haber elegido también variables temporales, pero por simplicidad, y también para evitar usar almacenamientos intermedios usaremos registros].
Un primer acercamiento para una rutina que lea operandos es esta:
procedure GetOperand();
{Extrae un operando. Actualiza la variable "resType".
Genera el código ensamblador necesario para que el operando siempre quede en un
registro.}
var
resCteStr: string;
begin
TrimSpaces();
//Captura primer operando, asumiendo que es el único
if srcToktyp = 3 then begin //Literal Número
resType := 1; //Integer
asmline('mov eax, ' + srcToken);
NextToken();
end else if srcToktyp = 4 then begin //Literal Cadena
resType := 2; //Tipo cadena
resCteStr := copy(srcToken,2,length(srcToken)-2); //Valor
DeclareConstantString(resCteStr);
//Carga en registro de cadena
asmline('invoke szCopy, addr ' + constrName + ', addr _strA');
NextToken();
end else if srcToktyp = 2 then begin //Identificador
//...
end else begin
MsjError := 'Error de sintaxis: ' + srcToken;
exit;
end;
end;Para esta rutina hemos creado una nueva variable global que nos dirá el tipo de dato al que pertenece el operando que hemos leído:
var resType : integer; //Tipo de dato: 1->integer. 2->string.Además necesitamos dos variables adicionales para reconocer las constantes de cadena:
var constrName : string; //Nombre de constante string usada actualmente
var nconstr : integer; //Número de constante string creadaY una rutina adicional para procesar a las constantes cadenas:
procedure DeclareConstantString(constStr: string);
{Inserta la declaración de una constante string, en la sección de datos, para
poder trabajarla.}
var
tmp: String;
begin
tmp := IntToStr(nconstr);
constrName := '_cstr' + tmp; //Nombre de constante
asmline('.data');
if constStr='' then begin
asmline(constrName+ ' db 0');
end else begin
asmline(constrName+ ' db "'+constStr+'",0');
end;
asmline('.code');
nconstr := nconstr + 1;
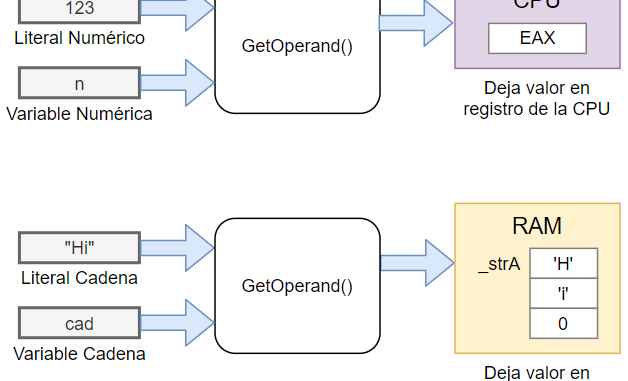
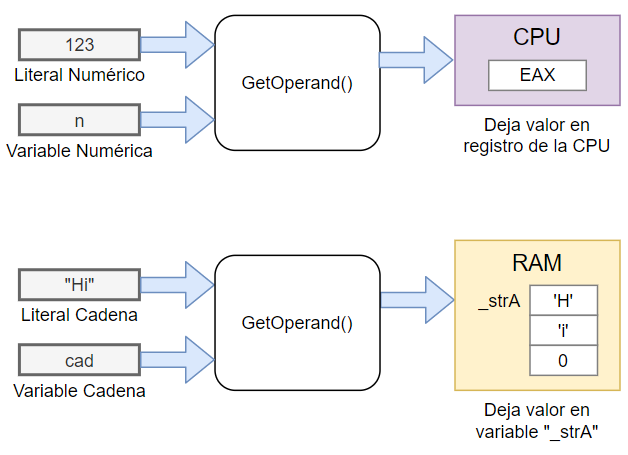
end;Nuestra rutina GetOperand() aún no reconoce identificadores. Solo reconoce a los literales de tipo numérico (como 123) o cadena (como «Hi»). El valor de los números se deja en el registro interno EAX de la CPU, mientras que el valor de las cadenas se copia en memoria en una variable interna que define el compilador y que sirve como una especie de registro para cadenas. El siguiente diagrama muestra el funcionamiento de GetOperand():
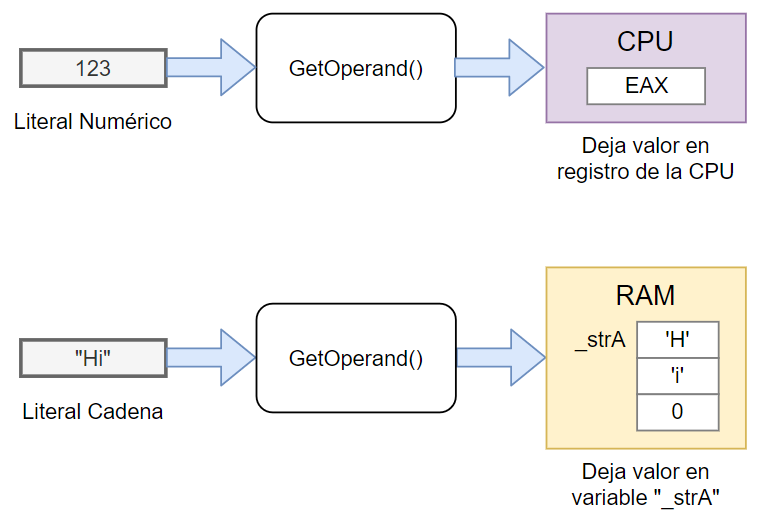
Lo ideal, y lo que hubiera facilitado la implementación del compilador, hubiera sido poder cargar números y cadenas en registros internos de la CPU, pero como las cadenas tienen un tamaño mayor (256 en nuestro lenguaje Titan) no se pueden ubicar en registros. Por eso se hace uso de la memoria RAM.
También se pudo haber uniformizado y cargar todos los valores en RAM, sean número o cadenas, pero sería una pérdida de tiempo para los números, guardarlos primero en RAM, para luego cargarlos a registro, y después moverlos nuevamente a RAM, que es la tarea más común cuando se procesan asignaciones como:
a = 123;10.4 Probando GetOperand()
Pongamos a prueba nuestra primera versión de GetOperand(). Para ello agreguemos una llamada a esta rutina desde ProcessBlock() que es donde se procesan las instrucciones:
procedure ProcessBlock;
//Procesa un bloque de código.
begin
while EndOfBlock()<>1 do begin
//Procesa la instrucción
GetOperand();
//Verifica delimitador de instrucción
Capture(';');
if MsjError<>'' then begin exit; end;
end;
end;Con este cambio obligaremos al compilador a leer operandos como si fueran instrucciones. No es la forma normal de trabajo, pero nos servirá para nuestras pruebas.
También necesitaremos incluir la declaración para nuestra variable interna «_strA», en el programa principal de Titan:
begin
//Abre archivo de entrada
AssignFile(inFile, 'input.tit');
Reset(inFile);
//Abre archivo de salida
AssignFile(outFile, 'input.asm');
Rewrite(outFile);
//Escribe encabezado de archivo
WriteLn(outFile, ' include \masm32\include\masm32rt.inc');
WriteLn(outFile, ' .data');
WriteLn(outFile, ' _strA DB 256 dup(0)');
MsjError := '';
NextLine(); //Prepara primera lectura.
NextToken(); //Lee primer token
ParserProgram(); //Procesa programa.
if MsjError<>'' then begin
//Genera mensaje en un formato apropiado para la detección.
WriteLn('ERROR: input.tit' + ' ('+IntToStr(srcRow) + ',' + IntToStr(idxLine)+'): ' + MsjError);
end;
//Terminó la compilación.
CloseFile(outFile);
CloseFile(inFile);
if MsjError='' then ExitCode:=0 else ExitCode:=1;
end.Con estos cambios ya estamos listos para probar la carga de operandos. Compilemos a Titan y luego compilemos un programa de pruebas con Titan:
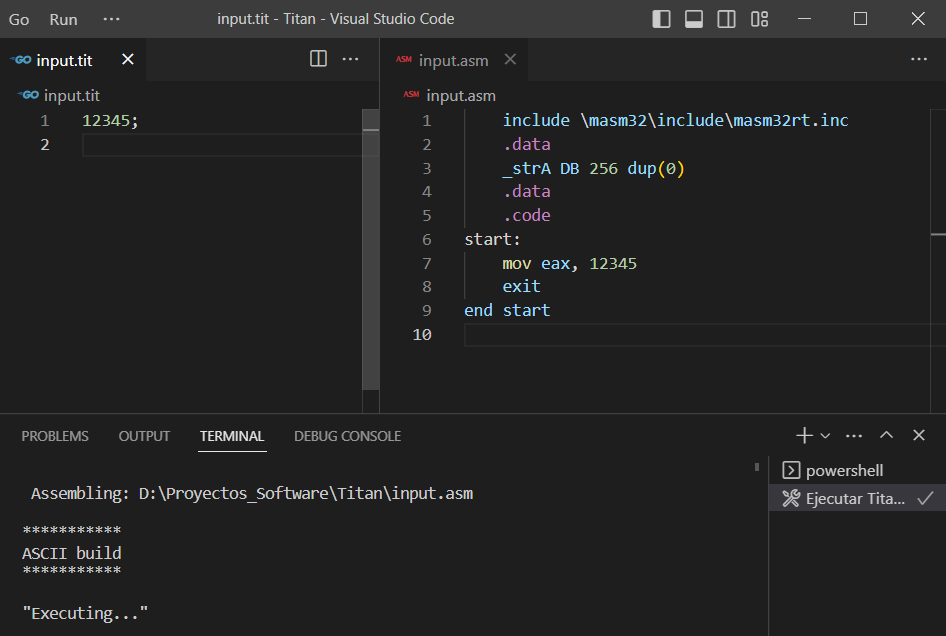
Con este código, podemos verificar que los literales numéricos se cargan en el registro EAX. Probemos ahora con un literal de cadena:

Los literales de cadena se definen primero como datos en la sección .DATA y se les asigna una etiqueta, que en nuestro caso es «_cstr0». Si se encuentran otros literales de cadena, tomarán el nombre «_cstr1», «_cstr2», etc. Esta tarea la realiza DeclareConstantString() con ayuda de la variable global «nconstr».
Una vez que se tiene en memoria al literal de cadena «Hola», se genera una instrucción ensamblador para copiar a esta cadena (con ayuda de la función «szCopy») al registro interno «_strA», que es donde se supone que deben quedar todos los operandos de tipo cadena.
Puede parecer redundante tener que cargar en memoria una cadena para luego copiar este valor a otra posición de memoria, pero hay que considerar que «_strA» es una zona de almacenamiento temporal que puede ir cambiando muchas veces su contenido.
Se puede optimizar este comportamiento, pero eso implicaría una mayor complejidad en la implementación del compilador. Nuestro método, que consiste de dejar en el registro EAX, el valor de todos los operandos numéricos y en «_strA» el valor de todos los operandos de cadena, simplificará el diseño de nuestro analizador de expresiones.
10.5 Procesando identificadores
Hasta este momento, nuestra rutina GetOperand() solo carga literales. Para poder reconocer a las variables, necesitamos procesar el caso de operandos que sean identificadores. Esto identificadores, dentro de las expresiones, solo podrán ser:
- Variables previamente declaradas.
- Funciones del sistema. Aún no implementado.
- Funciones definidas por el usuario. Aún no implementado.
Como aún no tenemos soporte para funciones dentro del lenguaje Titan, asumiremos que cualquier identificador debe referirse a una variable.
Para el reconocimiento de variables debemos implementar, primero, una función de búsqueda para determinar si un identificador corresponde a una variable. A esta función la llamaremos FindVariable() y tiene el siguiente código:
procedure FindVariable();
// Busca la variable con el nombre que está en "srcToken", y actualiza las variables:
// "curVarName", "curVarType", y "curVarArSiz".
// Si no encuentra, devuelve cadena vacía en "curVarName".
var
tmp : string;
contin: integer; //Bandera para continuar bucle.
curVar: integer; //Índice de variable.
begin
curVar := 0;
tmp := varNames[curVar];
if tmp=srcToken then begin contin:=0; end else begin contin:=1; end;
while contin=1 do begin
curVar := curVar + 1;
if curVar = 256 then begin break; end;
tmp := varNames[curVar];
if tmp=srcToken then begin contin:=0; end else begin contin:=1; end;
end;
//Verifica si encontró
if contin=0 then begin
curVarName := varNames[curVar];
curVarType := varType[curVar];
curVarArSiz := varArrSiz[curVar];
exit; //"curVar" contiene el índice
end;
//No encontró
curVarName := '';
end;La búsqueda, como es de esperar, se realiza sobre el arreglo varNames[] que es el contenedor de los nombres de todas las variables globales declaradas, como se indicó en el Capítulo 9. Esta función requiere que usemos unas variables globales adicionales, donde devolveremos el resultado de la búsqueda:
//Variable de trabajo
var curVarName : string;
var curVarType : integer; //Tipo de dato: 1->integer. 2->string.
var curVarArSiz: integer;Con esta función de búsqueda implementada, ya podemos proponer nuestro primer código para reconocimiento de variables dentro de GetOperand():
procedure GetOperand();
{Extrae un operando. Actualiza la variable "resType".
Genera el código ensamblador necesario para que el operando siempre quede en un
registro.}
var
resCteStr: string;
vName : string;
vType : Integer;
begin
TrimSpaces();
//Captura primer operando, asumiendo que es el único
if srcToktyp = 3 then begin //Literal Número
resType := 1; //Integer
asmline('mov eax, ' + srcToken);
NextToken();
end else if srcToktyp = 4 then begin //Literal Cadena
resType := 2; //Tipo cadena
resCteStr := copy(srcToken,2,length(srcToken)-2); //Valor
DeclareConstantString(resCteStr);
//Carga en registro de cadena
asmline('invoke szCopy, addr ' + constrName + ', addr _strA');
NextToken();
end else if srcToktyp = 2 then begin //Identificador
//Busca variable
FindVariable(); //Actualiza "curVarName", "curVarType" y "curVarArSiz".
if curVarName = '' then begin
MsjError := 'Identificador desconocido: ' + srcToken;
exit;
end;
//Es una variable. Podría ser un arreglo.
vName := curVarName; //Guarda porque se puede modificar con ReadArrayIndex().
vType := curVarType; //Guarda porque se puede modificar con ReadArrayIndex().
NextToken();
TrimSpaces();
if vType= 1 then begin //Variable entera
asmline('mov eax, ' + vName); //Carga en registro
end else begin //Variable cadena
asmline('invoke szCopy, addr ' + vName + ', addr _strA');
end;
resType := vType; //Tipo del resultado
end else begin
MsjError := 'Error de sintaxis: ' + srcToken;
exit;
end;
end;Con este código adicional (resaltado en naranja) ya podemos reconocer variables que hayan sido declarados con «var».
Compilemos y probemos un programa en Titan que incluya una variable entera y otra de cadena:
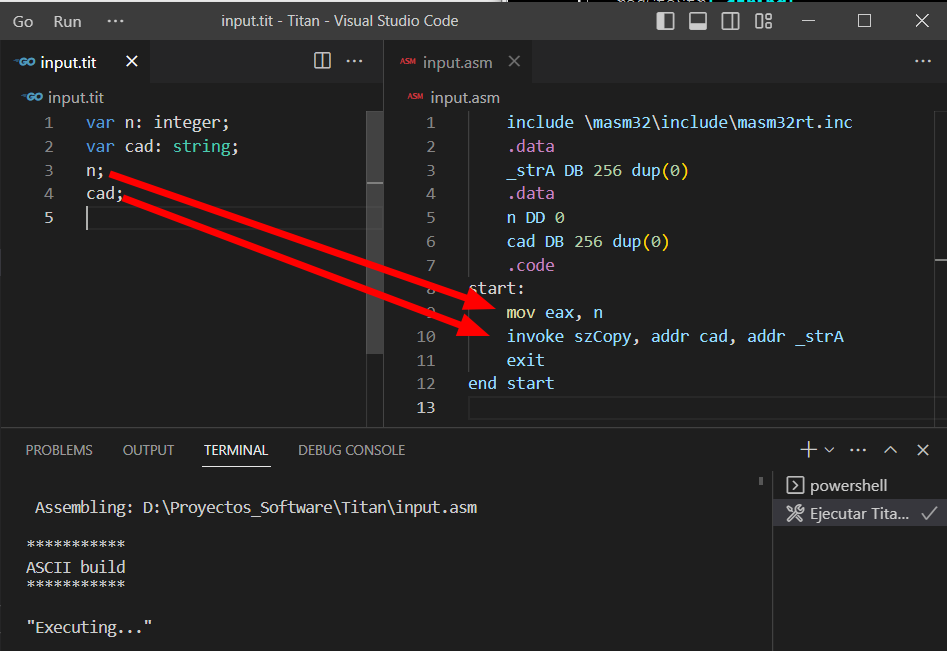
Se puede apreciar que estamos siguiendo la misma norma para la carga de variables, que usamos para los literales, de acuerdo con el tipo de dato. Al final cualquier operando terminará en el registro EAX de la CPU o en la variable «_strA» de la RAM. A estas ubicaciones las llamaremos «Registros de Trabajo».
Actualizando el diagrama de la figura 10.2, tendríamos:
10.6 Cambios finales
Nuestra rutina GetOperand() es bastante completa para cargar operandos en los registros de trabajo, pero cuando implementemos el evaluador de expresiones (Capítulo 12), necesitaremos operar sobre dos operandos. Para facilitar el manejo de dos operandos, necesitaremos otro par de registros de trabajo. Estos serán:
- Registro EBX -> Para operandos numéricas.
- Variable _strB -> Para operandos de cadena.
En el programa principal de Titan, necesitaremos incluir la declaración de la nueva variable «_strB» que nos servirá como el segundo registro de trabajo para cadenas.
begin
//Abre archivo de entrada
AssignFile(inFile, 'input.tit');
Reset(inFile);
//Abre archivo de salida
AssignFile(outFile, 'input.asm');
Rewrite(outFile);
//Inicia banderas
nVars := 0; //Número inicial de variables
srcRow := 0; //Número de línea
nconstr := 0;
//Escribe encabezado de archivo
WriteLn(outFile, ' include \masm32\include\masm32rt.inc');
WriteLn(outFile, ' .data');
WriteLn(outFile, ' _strA DB 256 dup(0)');
WriteLn(outFile, ' _strB DB 256 dup(0)');
MsjError := '';
NextLine(); //Prepara primera lectura.
NextToken(); //Lee primer token
ParserProgram(); //Procesa programa.
if MsjError<>'' then begin
//Genera mensaje en un formato apropiado para la detección.
WriteLn('ERROR: input.tit' + ' ('+IntToStr(srcRow) + ',' + IntToStr(idxLine)+'): ' + MsjError);
end;
//Terminó la compilación.
CloseFile(outFile);
CloseFile(inFile);
if MsjError='' then ExitCode:=0 else ExitCode:=1;
end.También hemos incluido unas líneas para la inicialización de ciertas variables globales que nos garantizarán que la declaración de variables y los literales de cadena se lean correctamente.
Con este último cambio, dejamos ya lista a GetOperand() y podría servir ya de soporte para implementar una rutina de evaluación de expresiones. No obstante, aún seguiremos agregándole funcionalidad adicional.
Como siempre el código completo de este Capítulo puede ser visto en https://github.com/t-edson/CreaTuCompilador, así como el de Capítulos anteriores.
En la siguiente entrega, daremos a GetOperand() la posibilidad de reconocer también a operandos de tipo arreglo antes de empezar a implementar al Analizador de expresiones.
![]() ¿Cómo citar este artículo?
¿Cómo citar este artículo?
- En APA: Hinostroza, T. (27 de mayo de 2019). Crea tu propio compilador – Cap. 10 – Carga de Operandos. Blog de Tito. https://blogdetito.com/2019/05/27/crea-tu-propio-compilador-parte-10/
- En IEEE: T. Hinostroza. (2019, mayo 27). Crea tu propio compilador – Cap. 10 – Carga de Operandos. Blog de Tito. [Online]. Available: https://blogdetito.com/2019/05/27/crea-tu-propio-compilador-parte-10/
- En ICONTEC: HINOSTROZA, Tito. Crea tu propio compilador – Cap. 10 – Carga de Operandos [blog]. Blog de Tito. Lima Perú. 27 de mayo de 2019. Disponible en: https://blogdetito.com/2019/05/27/crea-tu-propio-compilador-parte-10/

Dejar una contestacion