12.1 Introducción
En el capítulo anterior vimos cómo cargar operandos de tipo arreglo en los registros de trabajo correspondientes, tanto para enteros como para cadenas.
Pero todo el manejo que puede lograr nuestro compilador hasta ahora, se queda solamente en la carga de operandos a registro o memoria, sin poder procesar realmente una operación aritmética o lógica.
En este Capítulo diseñaremos e implementaremos un verdadero Analizador-Generador para las expresiones aritméticas, que, a pesar de su simplicidad, nos permitirá entender cómo funcionan los Analizadores de expresiones más completos que se usan en los compiladores modernos.
12.2 Teoría de Compiladores
Representación intermedia
Una representación intermedia es solo un lenguaje especial que se usa como apoyo en la traducción de un código fuente, generalmente de alto nivel, a uno de bajo nivel, es decir, en el proceso de compilación. Como este lenguaje está entre dos lenguajes, es que se le suele llamar Lenguaje Intermedio o Representación Intermedia.
Una característica fundamental de una representación intermedia (IR) es que se trata, precisamente, de «una representación» del código fuente en alguna etapa avanzada de procesamiento. Otra característica es que una IR se diseña para adaptarse bien al trabajo para el cual será usado. Por ejemplo, una IR usada para la generación de código, debe tener una estructura que facilite la creación de código directamente, sin preocuparse de la existencia de errores léxicos o sintácticos.
Las representaciones intermedias se han usado en compiladores e intérpretes prácticamente desde su nacimiento[1. En los primeros intérpretes de Basic, se solía «tokenizar» el código fuente antes de almacenarlo para su interpretación posterior] y hoy en día, casi todos los compiladores actuales usan algún tipo de representación intermedia, lo que es ya un indicio de la utilidad de esta tecnología. Inclusive el lenguaje ensamblador, o el mismo lenguaje C, pueden considerarse un tipo de representación intermedia cercana al código binario.
Mucha de la teoría desarrollada para compiladores trabaja en algún tipo de representación intermedia como el árbol de sintaxis o código de tres direcciones, lo que nos indica la importancia que tienen los lenguajes intermedios en el desarrollo de compiladores.
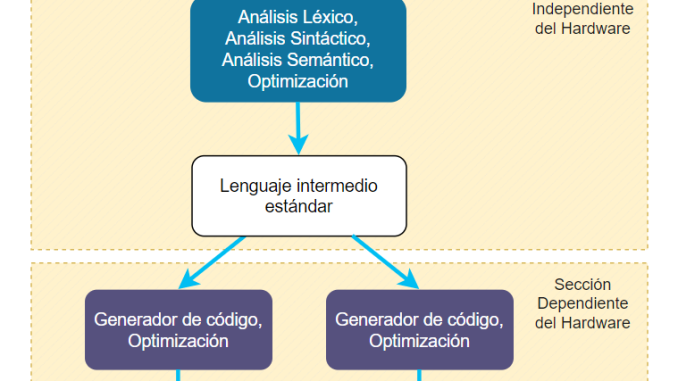
A pesar de que no es usual, es posible usar un lenguaje intermedio para cada fase de un compilador, como se muestra en la siguiente figura:
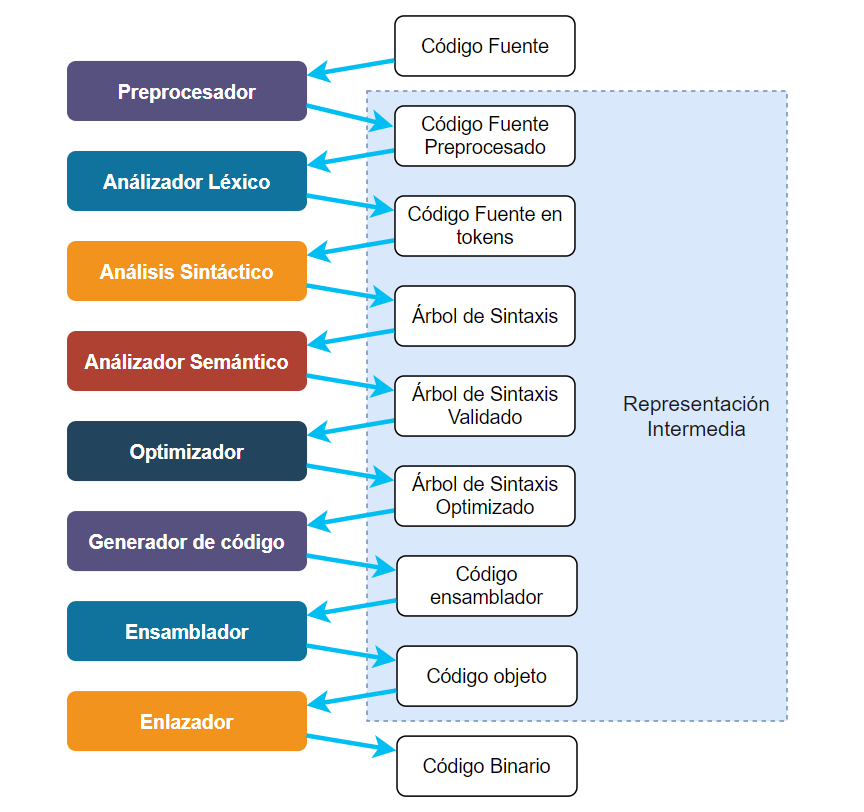
Algunos lenguajes intermedios, como el árbol de sintaxis, son más o menos estándar, pero cada compilador puede definir sus propias representaciones intermedias.
Las primeras representaciones intermedias de un compilador son las más «independientes del hardware», es decir, que podrían usarse sin cambios, o cambios mínimos, para un compilador que compile para otra CPU o arquitectura.
El diagrama mostrado es solo representativo. No todos los compiladores tienen las mimas fases ni las mismas representaciones intermedias. En algunos casos, varias fases pueden trabajar sobre la misma representación intermedia o algunos compiladores pueden incluir más o menos fases, y más o menos representaciones intermedias. Además, no todos los compiladores incluyen preprocesador y no todos llegan hasta la generación de Código Binario.
Los compiladores de una sola pasada (como nuestro compilador Titan) pueden inclusive, no usar ninguna representación intermedia [2. No estamos considerando el código ensamblador como una representación intermedia porque nuestro compilador funciona generando ensamblador como lenguaje de salida] porque la generación de código se hace directamente en la fase de Análisis.
Y aquí puede caber la pregunta ¿Qué tan importante es usar representaciones intermedias?
Es seguro que quien haya intentado realizar un compilador medianamente complejo y con opciones de optimización, entenderá la necesidad de usar representaciones intermedias, por la gran ventaja que ofrecen, especialmente en la generación y optimización de código. Su utilidad se puede entender mejor viendo las ventajas y desventajas que ofrece.
12.3 Clasificación de las expresiones en Titan
En el capítulo 10 se explicó la estructura de las expresiones en general, y aunque, en algunos compiladores, como los de lenguaje C, todas las expresiones se tratan de forma uniforme; en nuestro compilador, para simplificar la implementación, trabajaremos con dos tipos de expresiones, de acuerdo a su ubicación dentro del código fuente:
EXPRESIONES EN ASIGNACIONES
Las expresiones dentro de las asignaciones serán las que se encuentran al lado derecho de la asignación, después del operador de asignación, como se muestra a continuación.
valor = 1;
num = x + y;La parte sombreada de verde corresponde a la expresión, dentro de una instrucción de asignación. En nuestro lenguaje las asignaciones no se considerarán expresiones, tan solo la parte derecha de la asignación.
Estas expresiones deben soportar a los operadores «+», «-» y «|».
Este es el tipo de expresiones son las que trataremos en este Capítulo.
EXPRESIONES EN CONDICIONALES
Las expresiones, que aparecerán dentro de las instrucciones condicionales, tendrán un tratamiento separado y un evaluador de expresiones también separado.
Ejemplos de estas expresiones se muestran a continuación:
if x>1 then
end;
if eof() = 1 then
end;Estas expresiones deben soportar a los operadores «=», «<>», «>», «>=», «<» y «<=».
Este tipo de expresiones se manejarán con un evaluador de expresiones adicional que implementaremos cuando trabajemos con las condicionales.
12.4 Estructura de las expresiones en Titan
Cuando decimos «Evaluador de expresiones», en realidad estamos usando la forma corta del nombre largo «Analizador léxico-sintáctico de expresiones y generador de código para su evaluación» y nos referimos a una rutina que hace precisamente lo que el nombre largo indica.
Normalmente, dentro de un compilador, las expresiones son evaluadas, por rutinas recursivas que pueden manejar muchos operandos y consideran la precedencia de operadores. Pero estas rutinas tienen un nivel de complejidad un poco alto,
En Titan implementaremos dos evaluadores de expresiones modestos que permita evaluar expresiones cortas de uno o dos operandos y un solo operador.
El primer evaluador de expresiones que implementaremos será el que procesa las expresiones de la parte derecha de las asignaciones, como se indica en la sección 12.3 . Algunos ejemplos de estas expresiones son las siguientes:
n1 + n2; //Expresión de dos operandos.
n1; //Expresión de un operando.Eso significa que, por ejemplo, la expresión «x + y + 1» será considerada inválida, lo cual no es una gran limitación si consideramos que esta expresión la podemos dividir en dos expresiones más simples.
En general, las expresiones que va a manejar nuestro evaluador pueden ser de dos formas:
- <operando1>
- <operando1><operador><operando2>
Donde cada operando puede ser a la vez:
- Un literal numérico o cadena.
- Una variable.
- Una llamada a una función del sistema o definida por el usuario
Las llamadas a funciones, aún no se ha implementado en nuestro compilador (Ver el código de GetOperand), pero debemos considerar este caso de los operandos en nuestra implementación del evaluador de expresiones.
El operador solo puede ser de los tipos:
- Operador de suma «+».
- Operador de resta «-«.
- Operador lógico OR «|».
Si surge la pregunta: ¿Por qué tan pocos operadores? La respuesta es: «Porque son los únicos que necesitaremos para escribir un compilador Titan» y, a estas alturas del desarrollo, el lector deberá recordar que uno de los objetivos de nuestro compilador es ser minimalista pero capaz de compilarse a si mismo.
Nada impide que el lector pueda imprimir sus propios operadores, especialmente, después de ver lo sencillo que resulta implementar el soporte para un operador nuevo.
12.5 El algoritmo del evaluador
El algoritmo de nuestro Evaluador de expresiones, se puede describir más o menos así:
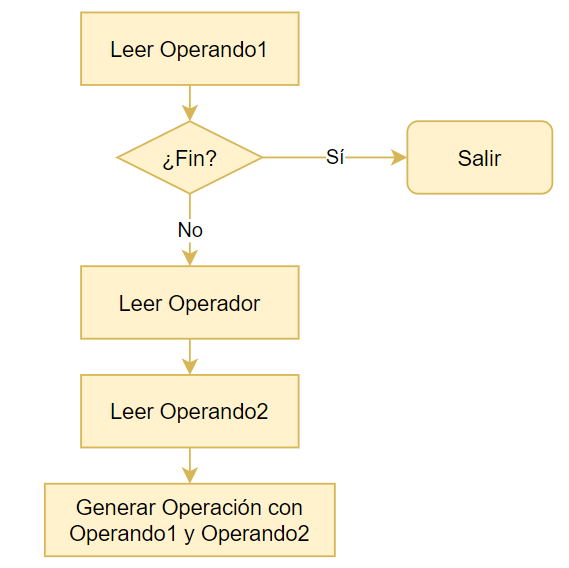
Para la lectura de operandos, usaremos nuestra rutina GetOperand() que ya hemos avanzado considerablemente. Pero debemos recordar que GetOperand() deja siempre el valor del operando en los registros EAX/_strA. Si usamos GetOperand() para leer dos operandos, podemos sobrescribir el primer operando leído. Para evitar ese problema usaremos el otro par de registros de trabajo EBX/_strB que ya habíamos definido en el Capítulo 10.
Con esta idea en mente, podemos crear dos procedimientos para la lectura de «Operando1» y «Operando2»:
procedure GetOperand1();
begin
GetOperand();
op1Type := resType;
end;
procedure GetOperand2();
begin
//Guarda Operando A en B
if op1Type = 1 then begin
asmline('mov ebx, eax'); //Copia Valor en B
end else begin
asmline('invoke szCopy, addr _strA, addr _strB');
end;
//Lee operando en A
GetOperand();
op2Type := resType;
end;La función de estos procedimientos es llamar a GetOperand(), elegir el juego de registros de trabajo y actualizar la variable de tipo correspondiente
Como ya habíamos adelantado, podemos observar que GetOperand2() guarda primero el valor del Operando1 en los registros EBX/_strB antes de llamar a GetOperand() para que deje sus valores en EAX/_strA.
Una limitación importante de GetOperand2() es que no debe modificar el valor de EBX o _strB (dependiendo del op1Type) para no perder el resultado del primer operando. Esta limitación se traduce en que las expresiones que vayamos a evaluar deben tener un «Operando2» sencillo, como puede ser un literal o una variable. De otra forma las expresiones se evaluarán de forma incorrecta.
Para almacenar el tipo de dato de los operandos leídos, necesitaremos dos nuevas variables globales:
var op1Type : integer; //Tipo de dato de Operando 1: 1->integer. 2->string.
var op2Type : integer; //Tipo de dato de Operando 2: 1->integer. 2->string.Agregando información sobre los registros usados, podemos actualizar el diagrama de flujo de nuestro Evaluador de Expresiones:
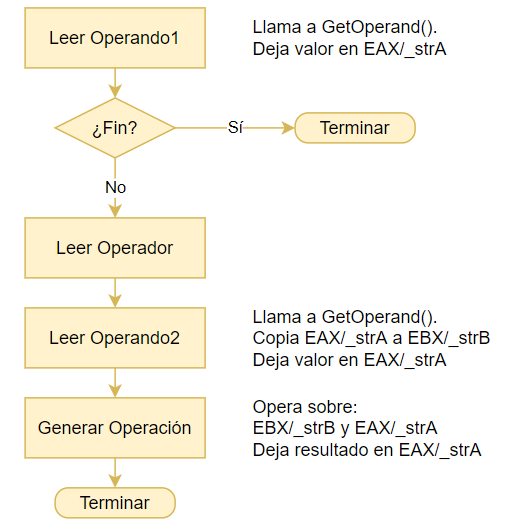
Observar que el resultado de la expresión se devuelve siempre en EAX/_strA, tanto si la expresión es de un solo operandos o de dos.
Este algoritmo permite leer expresiones de uno o dos operandos, pero no expresiones de más operandos. Sin embargo, para leer más operandos, basta con agregar un pequeño bucle de tipo «WHILE hay más operadores» justo antes del bloque «Leer operador», porque de todas formas, se espera que el bloque final deje el resultado en los registros de trabajo, tal cual lo hace «Leer Operando1».
12.6 Procedimientos para las operaciones
Para poder implementar el bloque «Generar Operación» del diagrama de flujo, primero vamos a crear tres procedimientos que trabajarán sobre los registros de trabajo ya indicados. Estos procedimientos se llamarán de acuerdo al tipo de operador binario que hallamos leído [3. El caso de las expresiones con operadores unarios, no lo veremos en este proyecto porque no es necesario para construir el compilador.]. Como solo soportaremos tres operadores, implementaremos tres procedimientos.
procedure OperAdd();
{Realiza la operación "+" sobre los operandos "EBX" y "EAX". Devuelve resultado
en "EAX" o en "_strA". Actualiza variable "resType".}
begin
if op1Type<>op2Type then begin
MsjError := 'No se pueden sumar estos tipos';
exit;
end;
//Son del mismo tipo
if op1Type = 1 then begin //Suma de enteros
resType := 1; //Devolvemos un entero.
asmline('add eax, ebx');
end else if op1Type = 2 then begin //Suma de cadenas
resType := 2; //Devolvemos una cadena
asmline('invoke szCatStr, addr _strA, addr _strB');
end;
end;
procedure OperSub();
{Realiza la operación "-" sobre los operandos "EBX" y "EAX". Devuelve resultado
en "EAX". Actualiza variable "resType".}
begin
if op1Type<>op2Type then begin
MsjError := 'No se pueden restar estos tipos';
exit;
end;
//Son del mismo tipo
if op1Type = 1 then begin //Resta de enteros
resType := 1; //Devolvemos un entero.
asmline('sub ebx, eax'); //Op1 - Op2
end else begin
MsjError := 'Solo se pueden restar enteros.';
end;
end;
procedure OperOr();
{Realiza la operación "OR" sobre los operandos "EBX" y "EAX". Devuelve resultado
en "EAX". Actualiza variable "resType".}
begin
if op1Type<>op2Type then begin
MsjError := 'No se pueden operar sobre estos tipos';
exit;
end;
//Son del mismo tipo
if op1Type = 1 then begin //Resta de enteros
resType := 1; //Devolvemos un entero.
asmline('or ebx, eax'); //Op1 OR Op2
end else begin
MsjError := 'No se puede aplicar OR sobre cadenas.';
end;
end;Como es de esperar el resultado se devuelve sobre los registros de trabajo: EAX para enteros, o _strA para cadenas.
Estas rutinas son las primeras de nuestro compilador que realmente hacen algo con los datos leídos, porque generan las instrucciones ensamblador que trabajan sobre los operandos, es decir, implementan las operaciones binarias (de un operador y dos operandos) que se realizan al momento de evaluar las expresiones:
Observar que, a diferencia del operador «-«, el operador «+» puede operar también sobre operandos de tipo cadena y realiza la concatenación de las cadenas en los operandos _strA y _strB, usando la API «szCatStr» que agrega la cadena _strB, al final de la cadena _strA. Hay que tener en cuenta que no se está realizando una verificación del tamaño del resultado, por lo que se podría generar un desborde o error en tiempo de ejecución si la cadena concatenada excede los 256 bytes.
12.4 El Evaluador de expresiones
Con estas nuevas rutinas implementadas, ya podemos hacer nuestro primer acercamiento a una rutina de evaluación de expresiones. A esta rutina la llamaremos EvaluateExpression() y más adelante la iremos completando con nuevas características:
procedure EvaluateExpression();
{Evalúa la expresión actual y genera el código necesario para dejar el resultado en el
registro EAX o _strA. Actualiza variable "resType"}
begin
//Toma primer operando
GetOperand1();
if MsjError<>'' then begin exit; end;
//Verifica si sigue algo, o si la expresión termina aquí.
if EndOfExpression() = 1 then begin exit; end;
//Hay más tokens. Extrae operador y operando
if srcToken = '+' then begin
NextToken(); //toma token
GetOperand2();
if MsjError<>'' then begin exit; end;
OperAdd(); //Puede salir con error
end else if srcToken = '-' then begin
NextToken(); //toma token
GetOperand2();
if MsjError<>'' then begin exit; end;
OperSub(); //Puede salir con error
end else if srcToken = '|' then begin
NextToken(); //toma token
GetOperand2();
if MsjError<>'' then begin exit; end;
OperOr(); //Puede salir con error
end else begin
MsjError := 'Error de sintaxis: ' + srcToken;
exit;
end;
end;
El algoritmo es el fiel reflejo del que se definió en la sección 12.5 y es bastante compacto. La parte más extensa corresponde al bloque «Generar Operación» y corresponde a la condicional de múltiples opciones.
Con esta rutina implementada, tenemos ya la posibilidad de que nuestro compilador pueda generar código para las expresiones soportadas. Solo hay un detalle a considerar, y es que no existe en nuestro lenguaje Titan alguna instrucción de tipo:
1+1;
De modo que para hacer pruebas llamando a EvaluateExpression() haremos una pequeña modificación sobre ProcessBlock() que ya antes habíamos «hackeado» para que llame a GetOperand(). El cambio a realizar sería solo reemplazar la llamada de GetOperand() por una llamada a EvaluateExpression():
procedure ProcessBlock;
//Procesa un bloque de código.
begin
while EndOfBlock()<>1 do begin
//Procesa la instrucción
EvaluateExpression();
//Verifica delimitador de instrucción
Capture(';');
if MsjError<>'' then begin exit; end;
end;
end;Lo que estamos logrando con este cambio, es que nuestro compilador reconozca solo expresiones como instrucciones. Esta no es la forma final de trabajo de Titan, pero servirá bien para nuestras pruebas.
Con este cambio, podremos ya probar la compilación de expresiones individuales como si fueran instrucciones válidas. Probemos con el siguiente ejemplo:
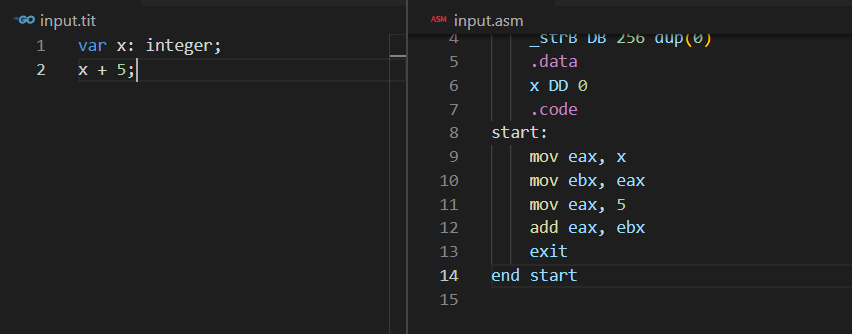
Cualquier lector observador podrá notar que este no es el código más optimizado para realizar este tipo de operaciones, pero como ya indicamos al inicio de esta obra, nuestro objetivo no es generar código optimizado.
El código generado corresponde a lo esperado: El primer operando cargado en EAX, y se mueve a EBX para cargar el segundo operando en EAX. Luego se incluye la instrucción de suma que devuelve el resultado en EAX, que es como el registro para retornar resultados. Es común, en los compiladores, usar varios registros para devolver resultados de expresiones. Luego estos resultados pueden ser guardados en otra variable o usado para calcular nuevas expresiones.
También podemos probar una expresión con cadenas:
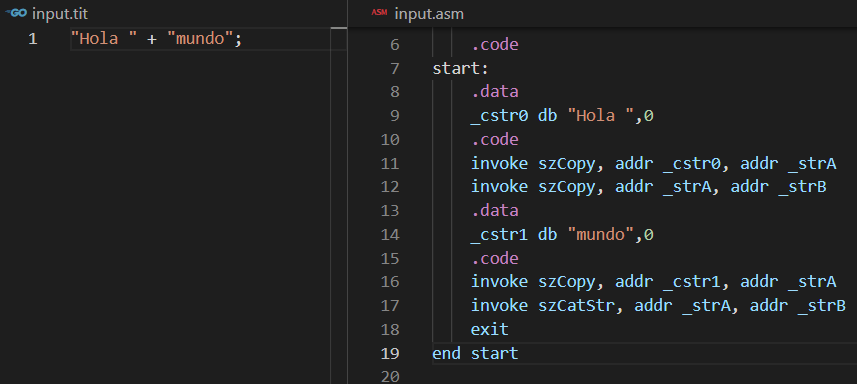
En este caso se está realizando una concatenación de cadenas y se aprecia que el código generado es similar al anterior excepto que se hace uso de zonas de datos temporales para las cadenas y se hace uso de las API de Windows para las operaciones de copia y concatenación.
Actualmente no podemos compilar expresiones más complejas que las que tienen dos operandos y un operador, pero eso no significa un gran problema porque las expresiones más complejas se pueden descomponer expresiones sencillas de dos o un operando.
![]() ¿Cómo citar este artículo?
¿Cómo citar este artículo?
- En APA: Hinostroza, T. (23 de septiembre de 2019). Crea tu propio compilador – Cap. 12 – El Evaluador de Expresiones. Blog de Tito. https://blogdetito.com/2019/09/23/crea-tu-propio-compilador-cap-12/
- En IEEE: T. Hinostroza. (2019, septiembre 23). Crea tu propio compilador – Cap. 12 – El Evaluador de Expresiones. Blog de Tito. [Online]. Available: https://blogdetito.com/2019/09/23/crea-tu-propio-compilador-cap-12/
- En ICONTEC: HINOSTROZA, Tito. Crea tu propio compilador – Cap. 12 – El Evaluador de Expresiones [blog]. Blog de Tito. Lima Perú. 23 de septiembre de 2019. Disponible en: https://blogdetito.com/2019/09/23/crea-tu-propio-compilador-cap-12/

Dejar una contestacion