
En la enseñanza de las matemáticas, los libros y muchos maestros, suelen omitir una parte de la enseñanza que es fundamental en el proceso de aprendizaje y que puede representar, o ha representado, un escollo insuperable para muchas personas, quienes probablemente, ni siquiera son conscientes de ello. Esta carencia se refiere a la correcta interpretación de los símbolos dentro del variado y heterogéneo lenguaje matemático.
Este tema se suele pasar por alto, por los siguientes motivos:
- Porque los mismos maestros desconocen esta interpretación y se centran solo en la enseñanza mecánica de las matemáticas.
- Porque es un tema poco estudiado y no resulta fácil transmitirlo y tampoco se encuentra explicado en los textos.
- Porque los expertos lo toman como algo muy elemental o que no se necesita explicar sino que se adquiere en el mismo proceso de aprendizaje.
- Porque está relacionado con la Filosofía y la Simbología, y como tal no se considera parte del conocimiento científico.
Introducción

Se dice que las matemáticas nacieron de la numerología, que el pensamiento lógico es la evolución del pensamiento místico. Si resumimos la historia, podría ser algo como esto:
Hace mucho tiempo, poco después del nacimiento de la conciencia, al hombre le empezó a atormentar lo desconocido. La naturaleza era misteriosa e implacable, y la vida era una aventura día a día.
El ser humano era poco más que un animal y como tal, le guiaba el instinto. Pero el animal humano desarrolló un arma poderosa, el lenguaje, el arte de asignar significado a los símbolos. El lenguaje produjo símbolos, y se usaron símbolos para representar a todo lo que el hombre veía o imaginaba.
En esa época salvaje, el hombre se inventó dioses y espíritus para darle sentido al mundo. ¿De qué otra forma se explicaría la lluvia o el trueno? La magia surgió como arma o defensa contra los poderes ocultos. Las artes adivinatorias se establecieron como una forma de interpretar los sueños, explicar el presente, o predecir el futuro a partir de los símbolos.
Con la aparición del lenguaje escrito, también se le dieron símbolos gráficos a los números. La numerología, el arte de asignar significados místicos a los números, había nacido.
Pero cuando el hombre descubrió que el universo seguía reglas, que existe orden en el caos, y que la lluvia se puede explicar mejor con un razonamiento que con un espíritu, empezó a nacer el pensamiento racional, y la lógica.
Pronto aprendimos que las mejores predicciones que podían darnos los números eran las que se apoyaban en la lógica y no en lo místico. Las matemáticas habían nacido.
Un poco de historia
Las matemáticas no aparecieron en este mundo como un saber místico, revelado en un libro sagrado y entregado a unos pocos dignos. A las matemáticas las fuimos descubriendo (algunos dirían «inventando») de a poco. A diferencia de lo que muchos puedan pensar, esta ciencia no nació con un lenguaje propio. Las matemáticas tuvieron que aprender a hablar su propia lengua.
Como la conocemos actualmente, es una ciencia que se mueve completamente el mundo abstracto o ideal, sin necesidad de conexión con el mundo físico concreto.
Pero no siempre fue así. El carácter abstracto de las matemáticas es posterior al pensamiento concreto. Los primeros matemáticos no fueron pensadores idealistas que veían un mundo imaginario y mágico de donde se podía crear una ciencia sino que fueron hombres prácticos que desarrollaron nociones básicas como la «cantidad» o la «suma» para cubrir algunas necesidades cotidianas como el de llevar la cuenta del ganado o comparar la cosecha.
En ese sentido, las matemáticas nacieron como una ciencia de aplicación totalmente pragmática, casi como lo es ahora la Física o Química.
El nacimiento de las matemáticas estuvo ligado al nacimiento de la geometría (Medida de la tierra), una ciencia que nació como una ayuda a la agricultura y a las necesidades arquitectónicas. <<Agregar Bibliografía>>.
Por muchos años, el avance de las matemáticas fue de la mano, con la geometría, que, a pesar de ser también una ciencia ideal, tiene un reflejo directo en el mundo físico, por su carácter dimensional. En ese sentido, cada resultado u operación matemática (como la multiplicación o la raíz cuadrada) podía verificarse también en su contraparte geométrica.
La geometría y las matemáticas estuvieron juntas hasta después de la edad media, inclusive hasta el siglo XIX. Durante todo ese tiempo, el lenguaje de las matemáticas era el mismo que el de la geometría antigua. Basta revisar la obra de Euclides para comprobar que aún no existía la notación algebraica moderna a la que estamos tan acostumbrados hoy por hoy, y que se hacía necesario una gran cantidad de texto para transmitir una idea.

Inclusive en 1687, año en que Newton escribió su «Principia mathematica», se puede corroborar que la notación matemática no estaba aún bien formada, y que las matemáticas seguían caminando al ritmo de la geometría, para transmitir sus conceptos, al menos para Newton:

Tuvo que pasar mucho tiempo para que las matemáticas se divorciaran de la geometría (también de la Física) y caminara a solas en su propio lenguaje y razonamiento. Solo cuando la matemática se separa de la geometría y desarrolla su propio lenguaje algebraico, es que empieza a crecer como verdadera ciencia abstracta [1. A pesar de que hoy en día, la matemática crece de forma separada de la Geometría, a la que se le considera una rama de ella, aún, muchos de sus conceptos se apoyan en la geometría para su mejor entendimiento.].
El lenguaje contemporáneo de las matemáticas se compone de símbolos, en su mayoría, operadores. Muy al contrario de lo que pueda pensarse, estos símbolos no aparecieron a la vez, ni siquiera en un periodo reducido de tiempo. Si bien, existieron símbolos numéricos desde las eras sumerias antediluvianas; la simbología actual data de épocas más recientes.
La numeración arábiga, que es de uso casi universal (diez cifras 1,2,3,4,5,6,7,8,9,0 con su notación posicional) fueron introducidos en Europa en el siglo X, cuando dominaban los números romanos. Un símbolo tan común como el que usamos para la raíz cuadrada no se usó hasta el mediados del siglo XVI.
Los símbolos aritméticos comunes de suma, resta y multiplicación que se nos hacen tan familiares, no fueron usados hasta inicios del siglo XVII, y se atribuyen al clérigo y matemático William Oughtred, quien también fue el primero en el uso de la letra griega π (PI) para denotar a la razón del perímetro de la circunferencia y su radio, pero este símbolo se puso de moda solo después de que Euler lo usara en su Introducción al cálculo infinitesimal de 1748.
Los símbolos más comunes para las operaciones de integración y diferenciación, la base del cálculo moderno, se crearon a mediados del siglo XVII y se deben a Leibnitz. La notación para el cálculo nació con el cálculo.
El lenguaje de las matemáticas
Las matemáticas tienen un lenguaje o notación escrita que se compone de símbolos y reglas para unir esos símbolo.
Pero no existe un único lenguaje escrito estándar para las matemáticas. Solo existen notaciones o símbolos más o menos estándar para expresar el pensamiento matemático.
Consideremos una fórmula sencilla como la Ley de cosenos:
c^2 = a^2 + b^2 - 2ab.cos(\alpha)
También podemos escribirla de las siguientes formas:
C^2 = A^2 + B^2 - 2ABcos(\alpha)
C^2 = A^2 + B^2 - 2AB \cdot cos(\alpha)
c^2 = a^2 + b^2 - 2ab \times cos(A)
c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot csn(A)
c^2 = a^2 +b^2 - 2ab cosA
Y no es solo que podamos cambiar el signo de multiplicación, el uso de las letras griegas, los paréntesis, o el nombre de las funciones trigonométricas. Inclusive es posible usar un idioma y alfabeto distinto, como el que usaban matemáticos de la antigüedad, sin que por ello la notación deje de ser matemática.
En el extremo de la versatilidad, el pensamiento matemático puede expresarse también de forma gráfica. La siguiente figura puede representar, ni más ni menos, que al Teorema de Pitágoras, y sin decir ni una palabra:
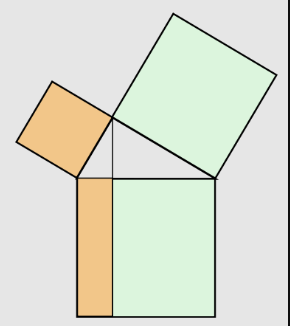
Y así como la simbología, tampoco las reglas son estándar.
Eso significa que cualquiera puede definir sus propios símbolos y reglas para expresar las mismas leyes o teoremas. La misma matemática se podría expresar en lenguaje extraterrestre sin que eso la convierta en otra ciencia. Al valor π, podemos llamarle con la letra que queramos y no dejará de ser π.
Desde luego que, si queremos entendernos mejor entre nosotros; es conveniente usar los símbolos y reglas que están más estandarizados. Algo así como tener que escribir en latín si se era un matemático de la edad media.
El carecer de reglas gramaticales universales o símbolos estandarizados , como si los tienen los lenguajes de programación de computadoras, trae consigo algunos incidentes, como el debate recurrente sobre si una expresión está bien evaluada o no, como es el caso mostrado de la siguiente figura:
6 \div 2(1+2)
¿El resultado es 9 o 1?
Ambos resultados son válidos. Lo que sucede es que en el primer caso se le está dando la misma precedencia (prioridad) al operador «÷» que a la multiplicación implícita entre el 2 y el (1+2), y se está evaluando de izquierda a derecha. En el segundo caso se le está dando mayor precedencia a la multiplicación implícita, que al operador «÷».
Inclusive se pueden obtener resultados diferentes, usando modelos distintos de calculadoras electrónicas.
Este es un caso de interpretación diferente de símbolos. Y nos recuerda que, aún en las matemáticas, hay que hacer hermenéutica.
Pero la falta de rigidez en el lenguaje de los números no debería verse como una debilidad sino más bien como una oportunidad para desarrollar la creatividad y hacer del lenguaje matemático una lengua viva, adaptable, evolutiva, en crecimiento y con aplicación a todos los campos del conocimiento.
Los lenguajes de programación
A diferencia de las matemáticas, los lenguajes de programación de computadoras, sí usan un lenguaje correctamente definido, a nivel léxico, sintáctico y semántico.
Si se define que el operador de suma para tipos de datos numéricos es el símbolo «+» (identificado por un código numérico único dentro de una tabla de caracteres), no hay posibilidad de usar otro símbolo. Además, una vez que se ha definido el alcance de un operador, ya no se puede cambiar posteriormente.
Un lenguaje de programación no solo define a todos los operadores existentes y su función precisa, sino que también indica la precedencia de cada operador y el orden de evaluación de las expresiones.
La siguiente tabla muestra algunos operadores del lenguaje C, ordenados por su precedencia:
| Símbolo | Descripción | Asociatividad |
|---|---|---|
[ ] ( ) -> . | Expresiones | De izquierda a derecha |
& * + - ~ ! | Operadores Unarios | De derecha a izquierda |
* / % | Multiplicación y división | De izquierda a derecha |
+ - | Sumas y restas | De izquierda a derecha |
< > <= >= | Relacional | De izquierda a derecha |
== != | Igualdad | De izquierda a derecha |
& | Operador de bit AND | De izquierda a derecha |
^ | Operador de bit OR exclusivo | De izquierda a derecha |
| | Operador de bit OR inclusivo | De izquierda a derecha |
&& | Operador lógico AND | De izquierda a derecha |
|| | Operador lógico OR | De izquierda a derecha |
= += -= *= /= %=^= |= | Asignación simple y compuesta | De derecha a izquierda |
Y lo mismo sucede con las variables. Los nombres de variables solo pueden usar los caracteres definidos (de un grupo finito) y siguiendo las reglas de creación de identificadores.
Por ejemplo, para el lenguaje Pascal, los identificadores se pueden definir usando la notación Backus Naur:
<identificador> ::= <letra> | <identificador> <letra> | <identificador> <dígito>
<letra> ::= «A» | «B» | «C» | «D» | «E» | «F» | «G» | «H» | «I» | «J» | «K» | «L» | «M» | «N» | «O» | «P» | «Q» | «R» | «S» | «T» | «U» | «V» | «W» | «X» | «Y» | «Z» | «a» | «b» | «c» | «d» | «e» | «f» | «g» | «h» | «i» | «j» | «k» | «l» | «m» | «n» | «o» | «p» | «q» | «r» | «s» | «t» | «u» | «v» | «w» | «x» | «y» | «z»
<dígito> ::= «0» | «1» | «2» | «3» | «4» | «5» | «6» | «7» | «8» | «9»
Esta notación, en lenguaje común, nos indica que los nombres de variables deben empezar solo con algunas de las letras indicadas, y continuar con alguna de esas letras o con algún dígito numérico.
Los lenguajes de programación, caen en la categoría de lenguajes formales, que es un campo de estudio que involucra a las matemáticas, la computación y la lingüística.
La abstracción de las matemáticas

VERDAD MATEMÁTICA 1: Las matemáticas tratan de elementos abstractos. Dichos elementos no son visibles, ni medibles con instrumentos.
Este hecho es válido para todas las entidades matemáticas.
Aunque es frecuentemente olvidado, es muy importante, y lo resalto para que quede claro: No se puede ver un número o una operación matemática.
Todo se mueve en el universo imaginario de las matemáticas, en donde «flotan» los números, variables, funciones, anillos, grupos o espacios vectoriales, y todos esos «fantasmas» que no se pueden ver ni tocar.
En clases de primarias se nos enseñan cosas como que podemos tener un «Conjunto de pollos negros» o que el «Conjunto de chanchos voladores» es un conjunto vacío.
Pero, estrictamente, no se puede tener un conjunto de pollos ni de chanchos, porque los pollos y chanchos (al menos como los conocemos) no son elementos abstractos. Son objetos concretos (sin ánimo de cosificar a los animales) que se pueden ver, tocar y hasta comer.
Otra cosa sería que cuando digamos «pollo» nos estemos refiriendo a una variable o una función o alguna otra entidad matemática verdadera.
Así que, cuando oigamos algo como «Un conjunto de pollos», pensemos que es una estrategia pedagógica para facilitar el entendimiento del conjunto, pero que no puede existir tal cosa en el universo prístino y puro de las matemáticas.
De otra forma empezarán a surgir preguntas extrañas como:
- Y si le pongo una mochila cohete al chancho ¿Ya es un chancho volador? o
- Y si un pollo se autodefine como un pato ¿Aún así pertenece al conjunto?
Mezclar nuestro mundo físico con el mundo ideal de las matemáticas origina estas contrariedades. Este punto es olvidado frecuentemente, creando confusión en los estudiantes, con el riesgo de hacer pensar que las matemáticas tienen inconsistencias de este tipo, lo cual es definitivamente falso.
Los símbolos matemáticos, como los números, representan a entes que viven solo en la mente, a pesar de que están ligados al concepto intuitivo y cotidiano de cantidad.
![]() ¿Cómo citar este artículo?
¿Cómo citar este artículo?
- En APA: Hinostroza, T. (17 de octubre de 2023). Matemáticas, el poder de los símbolos – Cap. 1. Blog de Tito. https://blogdetito.com/2023/10/17/matematicas-el-poder-de-los-simbolos-cap-1/
- En IEEE: T. Hinostroza. (2023, octubre 17). Matemáticas, el poder de los símbolos – Cap. 1. Blog de Tito. [Online]. Available: https://blogdetito.com/2023/10/17/matematicas-el-poder-de-los-simbolos-cap-1/
- En ICONTEC: HINOSTROZA, TIto. Matemáticas, el poder de los símbolos – Cap. 1 [blog]. Blog de Tito. Lima Perú. 17 de octubre de 2023. Disponible en: https://blogdetito.com/2023/10/17/matematicas-el-poder-de-los-simbolos-cap-1/

Dejar una contestacion