OPAMP – Cap. 2 – Modo común y modo diferencial

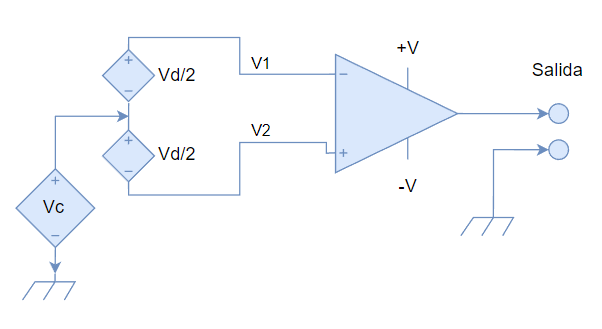
Dependiendo de cómo se aplica el voltaje de entrada a un OPAMP o a un amplificador diferencial, se puede diferenciar dos modos de operación:

• Modo diferencial. Referido al funcionamiento amplificando la diferencia de voltajes a la entrada.
• Modo común. Referido al funcionamiento amplificando el voltaje común de las entradas.

En la mayoría de aplicaciones con OPAMP, y en algunos ejercicios prácticos, no se tienen en cuenta estos modos de operación, pero es muy importante, tenerlos en cuenta, si pretendemos realizar diseños que con Amplificadores Operacionales.

2.1 El modo diferencial

Este es el modo normal de trabajo de un OPAMP, pues es en este modo en donde se usa al OPAMP como un verdadero amplificador diferencial.

Consideremos el siguiente circuito, en donde se aplica una tensión Vd entre las entradas de un OPAMP:

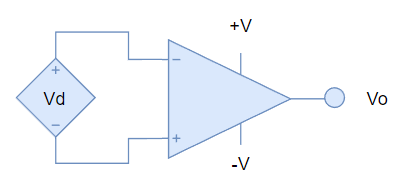
En este modo el OPAMP estará amplificando la diferencia de voltajes entre las entradas que sería Vd. El voltaje ideal de salida sería:

V_o = A_d.V_d 

El valor Ad es llamado Ganancia en modo diferencial o Ganancia en lazo abierto. Normalmente es un valor muy alto, del orden de cientos de miles, por lo que resulta más cómodo expresarlo en decibelios.

El voltaje Vo sería el voltaje de la salida con respecto a la tierra de fuente de alimentación, en un caso ideal.

En un caso más real, aparecería un voltaje de desplazamiento:

V_o = A_d.V_d + V_{offset}

En la práctica, este voltaje adicional que aparece en la salida (que puede ser positivo o negativo), se compensa realimentando al OPAMP o corrigiéndolo con una línea adicional del OPAMP.

2.2 El modo común

Consideremos la conexión de un OPAMP en donde juntamos las entradas (ponemos el voltaje diferencial a cero) realizando un cortocircuito de las entrada, como se muestra en el siguiente circuito.

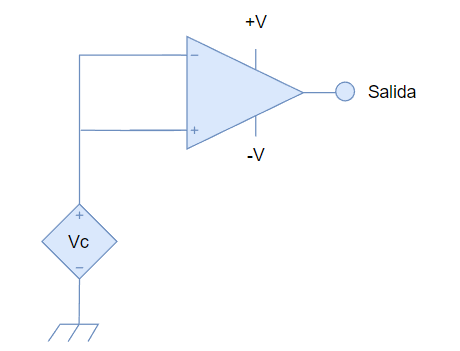
Vc funciona como un voltaje de entrada, pero al ser el voltaje común a ambas entradas, se le denomina voltaje en modo común.

En un caso ideal, el voltaje de salida debería ser cero siempre, independientemente del valor de Vc:

V_o = 0

En la práctica, el voltaje de salida presenta un valor diferente de cero y es una función del valor de Vc:

V_o = f(V_c) + V_{offset}

La función f(Vc) real puede ser una función no lineal, pero se puede simplificar como se muestra en la sección 2.4.

Puede pensarse que un OPAMP trabajando en modo común, como se muestra en la figura 2, es solo un caso especial e ideal, pero en la práctica, los OPAMP trabajan, en el 90% de los casos, con valores de V1 y V2 muy cercanos (menos de un milivoltio) de modo que se puede asumir que se encuentran en modo común, tal como se muestra en la figura 2.

2.3 Entrada balanceada y desbalanceada

Para una análisis de un caso combinado, consideremos el siguiente circuito:

En este diagrama, más detallado, mostramos el modelo eléctrico de una entrada balanceada con respecto al punto de tierra. No todos los casos en donde se usan amplificadores diferenciales tienen las entradas de este tipo, pero este modelo sencillo nos servirá como objeto de estudio.

Del diagrama podemos obtener el voltaje diferencial:

V_d = V_2 - V_1

Se podría argumentar que en este caso, estrictamente no hay un voltaje en modo común, porque V1 y V2 son diferentes pero se puede obtener una aproximación usando el promedio del voltaje de las entradas:

V_c = \frac{V_1 + V_2}{2}

Lógicamente, mientras más cercanos sean V1 y V2 (como suele pasar en la mayoría de casos), más se acerca este valor al de un verdadero voltaje en modo común.

Existen diversas conexiones que tener a la entrada de un OPAMP, además de la entrada balanceada que hemos mostrado.

Solo, a título de ejemplo, consideremos el siguiente caso:

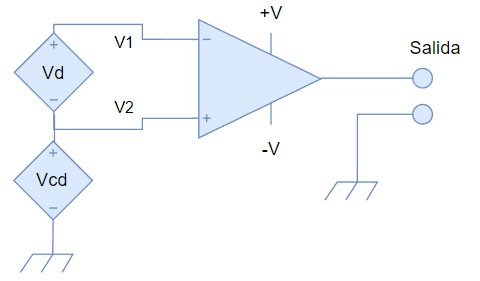
Esta conexión de entrada es una conexión desbalanceada, pero podemos asumir los valores de Vc y Vd usando las mismas formulas anteriores.

En general, como el voltaje diferencial es casi siempre muy pequeño, importa poco si la entrada trabaja de forma balanceada o desbalanceada, porque, mientras Vd sea muy pequeño podemos asumir que estamos trabajando siempre en modo común.

2.4 Rechazo al modo común CMRR

En condiciones ideales, la salida de un Amplificador Operacional debería ser simplemente función del voltaje diferencial:

V_o = A_d . V_d  

Lo que significa que la salida solo es dependiente del voltaje en modo diferencial (multiplicado por una ganancia en modo diferencial Ad), sin considerar el modo común. Pero los amplificadores diferenciales reales no son totalmente independientes del voltaje en modo común. Dependiendo de la construcción del amplificador diferencial, la salida real sería una función de Vd y Vc:

V_o = f(V_d,V_c)

En un caso simple, la salida sería una simple función lineal de Vd y Vc:

V_o = A_d.V_d + A_c.V_c

En esta fórmula aparece también de una ganancia para el modo común Ac. Cuanto más bajo sea el valor de Ac, mejor será el amplificador diferencial.

En condiciones normales, el valor de Ac es mucho menor que uno, de modo que, en lugar de amplificación, hablamos de atenuación o rechazo en modo común.

Precisamente un parámetro importante de los amplificadores diferenciales (y también de los amplificadores operacionales) es el rechazo en modo común o CMRR (Common-Mode Reject Ratio), que es la relación de Ad y Ac, expresado en decibelios:

CMRR = 20. \log_{10}( \frac{A_d}{A_c})

Al ser Ad, un valor mucho mayor que Ac, CMRR debe ser un valor positivo y grande.

Valores comunes de CMRR son 80db, 90db o mayores.

El valor del CMRR, y las condiciones de medida, se lee de las hojas técnicas del OPAMP. La siguiente imagen muestran un fragmento de las hojas técnicas de los OPAMP de la serie TL07xH (TL071H, TL072H y TL074H):

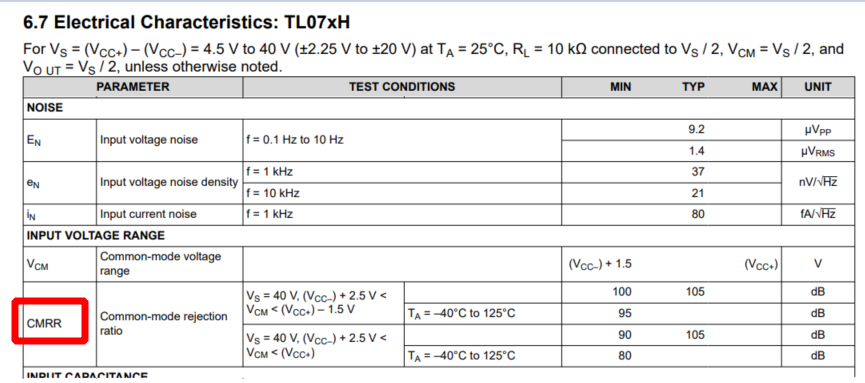
Para estos OPAMP, se lee que el CMRR típico es de 105dB, pero el valor mínimo depende de las condiciones de medida. El valor máximo no se indica porque tal vez es muy variable y no es muy importante, en realidad, en comparación al CMRR mínimo.

Tener un CMRR alto significa que el OPAMP se acerca más a la de un circuito ideal, y nos puede ayudar en la supresión de ruidos o a obtener medidas de voltaje más exactas.

2.5 Ejercicios

EJERCICIO 1. Buscar en los «Datasheet», cuál es el CMRR del Amplificador Operacional TL081.

EJERCICIO 2. Un OPAMP tiene una ganancia en modo diferencial de 100 mil y una ganancia en modo común de 30. Calcular el CMRR.

Solución:

Con los datos indicados, solo basta con aplicar la fórmula.

CMRR = 20. \log_{10}( \frac{A_d}{A_c}) \\
A_d = 100000 \\
A_c = 30 \\
CMRR = 20. \log_{10}( \frac{100000}{30}) \\
CMRR = 20. \log_{10}( 3333.33) \\
CMRR = 70.4 db \\

EJERCICIO 3. El OPAMP 741 tiene una ganancia en Modo diferencial de 200mil. Si el CMRR es de 90dB, ¿Cuánto vale su ganancia en Modo común?

Solución:

La respuesta se haya reemplazando directamente los datos en la fórmula del CMRR.

CMRR = 20. \log_{10}( \frac{A_d}{A_c})\\
A_d = 200000\\
90 = 20. \log_{10}( \frac{2.10^5}{A_c}) \\
4.5 = \log_{10}( \frac{2.10^5}{A_c}) \\
10^{4.5} =  \frac{2.10^5}{A_c}\\
A_c =  6.3\\

Notar que la ganancia Ac calculada, se ha redondeado al primer dígito. Este redondeo es común en dispositivos como los OPAMP, en donde los parámetros en lazo abierto son solo aproximados y muy variables de un dispositivo a otro.

EJERCICIO 4. Según datos de la hoja técnica, el TL071 tiene un CMRR de 100db típico. Si la ganancia en modo diferencial se midió en 120db. ¿Cuánto será aproximadamente su ganancia en modo común en decibelios?

Solución:

CMRR = 86db \\
A_d = 120db \\

Primero convertimos la ganancia Ad, de decibelios a un factor simple. Usamos la forma de conversión de decibelios:

Ganancia_{db} = 20. \log_{10}(Ganancia_{factor})\\
120 = 20. \log_{10}(Ganancia_{factor})\\
Ganancia_{factor} = 10^6 = Ad

Con este valor reemplazamos en la fórmula de CMRR:

CMRR = 20. \log_{10}( \frac{A_d}{A_c})\\
100 = 20. \log_{10}( \frac{10^6}{A_c}) \\
5 = \log_{10}( \frac{10^6}{A_c}) \\
10^5 =  \frac{10^6}{A_c}\\
A_c =  10\\

Ahora solo basta con convertir este valor a decibelios, lo que nos daría 20db.

Otra forma más directa de obtener el mismo resultado sería, usando las propiedades de los logaritmos. Si sabemos que el CMRR es de 100dB, y si el Ad es de 120dB, solo bastaría resta 120db – 100db para obtener el valor de Ac.