OPAMP – Cap. 7 – Análisis de circuitos

El análisis de circuitos con OPAMP (o resolución de circuitos) es un caso particular de análisis de circuitos que requiere de un método adecuado si queremos llegar a buen puerto.

A pesar de que existen diversos métodos de análisis muy útiles, no existe una fórmula mágica e infalible de resolución para todos los casos.

En este Capítulo se propone un proceso natural de análisis y un método de resolución que se sustenta en el modo en que funciona un OPAMP real y en simples reglas de resolución de circuitos eléctricos.

7.1 El proceso

Nuestro proceso de análisis de circuitos con OPAMP, tendrá hasta tres pasos:

1. La identificación del circuito.
2. La resolución del circuito.
3. Definición de rango de funcionamiento y saturación.

Con la resolución del circuito se podría terminar el proceso si asumimos que el OPAMP es ideal y así obviaríamos el paso 3.

En la fase de resolución de circuitos, usaremos solo dos fundamentos teóricos:

• FT1: Concepto de un OPAMP:
  • Es un amplificador diferencial de alta ganancia.
  • Tiene alta impedancia en cualquiera de sus entradas.
• FT2: Leyes básicas de circuitos eléctricos:
  • Leyes de Kirchhoff.
  • Ley de Ohm.

Si conocemos la teoría de estos dos ítems, no tendremos mayor problema en la resolución de circuitos. La siguiente figura esquematiza el proceso descrito:

Notar que nuestra definición de OPAMP corresponde al de un OPAMP real, no ideal (por eso usamos los términos «alta ganancia» y «alta impedancia»), por lo tanto, nuestro enfoque en el análisis se orientará a la resolución de circuitos reales, aunque usando las aproximaciones numéricas que son comunes en ingeniería.

7.2 Identificación del circuito

La identificación del circuito consiste en determinar ante qué tipo de circuito estamos. El siguiente diagrama indica los diversos tipos de circuitos que debemos considerar:

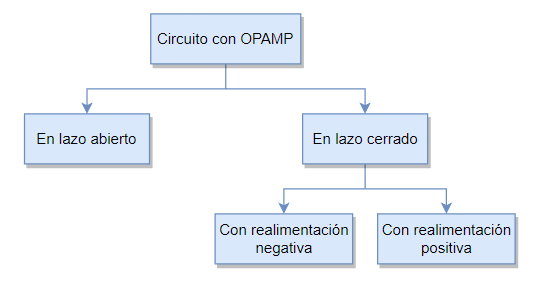
Para determinar si estamos ante un caso de lazo abierto o lazo cerrado, debemos hacernos la siguiente pregunta: ¿Un cambio en la salida puede influenciar, aunque sea mínimamente, en el voltaje que recibe la entrada?

Como ejemplo, consideremos el siguiente circuito:

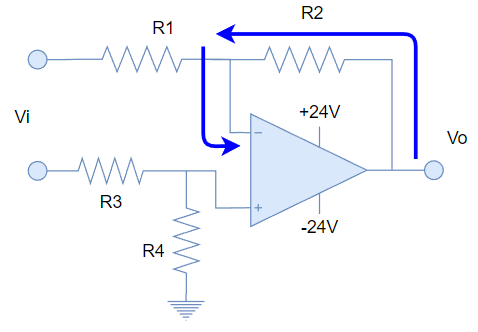
Aquí hay una conexión directa de la salida a la entrada inversora a través de R2 (en forma de divisor de voltaje con R1 y R2), así que se trata de un típico caso de lazo cerrado.

Analicemos ahora otro circuito un poco más elaborado:

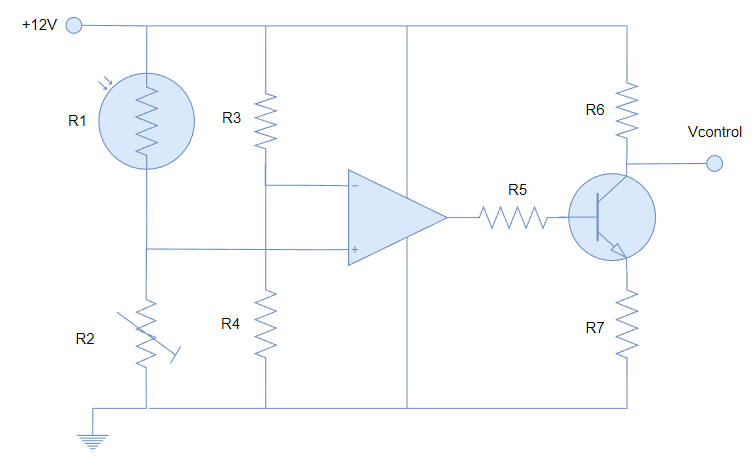
Aunque podría parecer que sí existe conexión eléctrica entre la salida y la entrada, este tipo de conexión sería solo a través de las líneas de alimentación, que, para nuestros fines, no se considera como una línea que pueda conducir algún tipo de señal [0. Resulta interesante saber que, en efecto, si la alimentación no está correctamente filtrada; la línea de alimentación se comportará como un camino por donde puede circular la señal.].

Así que, si no consideramos las líneas de alimentación, este circuito sería un caso de OPAMP en lazo abierto.

Si no se tiene certeza sobre qué a qué tipo de circuito nos enfrentamos, podemos hacer el ejercicio mental de variar la salida, en forma extrema y analizar si hay algún cambio en la alimentación.

Finalmente, si es que hemos identificado el caso de Lazo cerrado, debemos además, identificar si estamos ante un caso de circuito realimentado positiva o negativamente, lo cual debería ser sencillo en la mayoría de casos. Para mayor información sobre los tipos de realimentación, podemos consultar el Capítulo 3.

7.3 Análisis en lazo Abierto

Este es, probablemente, el caso más simple de análisis de circuitos con OPAMP, y sin embargo, muchos textos no lo consideran en su contenido.

Para analizar este tipo de circuitos, debemos tratar al OPAMP como lo que es: Un amplificador diferencial de alta ganancia y aplicamos la fórmula de salida, que se dio en la sección 4.2:

\begin{align}
V_o = A_d.(V_d+V_{offset})
\end{align} 

Donde Vd es el voltaje diferencial a la entrada del OPAMP, que equivale a la resta de voltaje entre la entrada no-inversora y la entrada inversora.

Partiendo de esta fórmula, ya se pueden analizar los circuitos de lazo abierto con OPAMP. Por ejemplo, intentemos analizar el siguiente circuito:

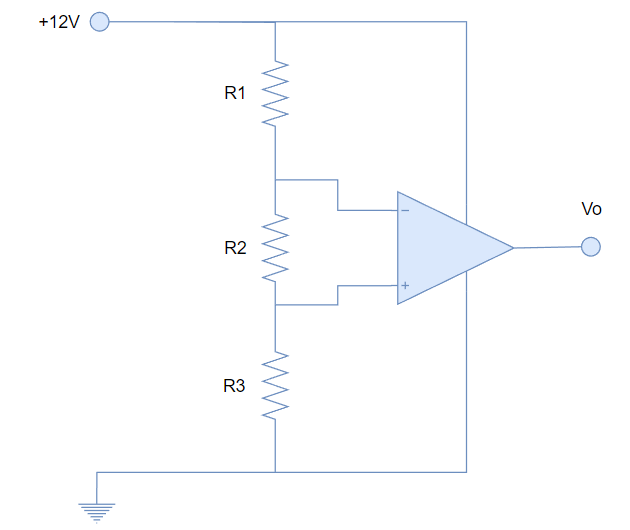
Primeramente podemos calcular el voltaje diferencial mediante la fórmula de división de tensión:

V_d = \frac{R2}{R1+R2+R3}

El voltaje de offset de entrada lo podemos obtener de las hojas técnicas del operacional. Aquí viene el primer inconveniente porque este valor no es exacto sino que varía mucho y resulta más conveniente trabajar con los límites.

SI nuestro operacional es, por ejemplo, el uA741, podemos leer de sus hojas técnicas que tenemos un Voltaje de offset máximo de 7.5mV, que puede ser positivo o negativo. Si nuestro voltaje diferencial Vd puede compensar a este Voltaje de offset, (ver ecuación 1) podríamos tener un valor cercano a cero en la salida. Pero lo más probable es que la salida se sature a nivel alto o bajo, que es lo normal en circuitos de lazo abierto. Lo más seguro para obtener un voltaje no saturado en la salida sería usar compensación de offset en el OPAMP (Ver Sección 4.2).

Por eso, los amplificadores de lazo abierto con OPAMP son poco usados. La única aplicación segura para lazo abierto sería como comparador, como en el siguiente circuito:

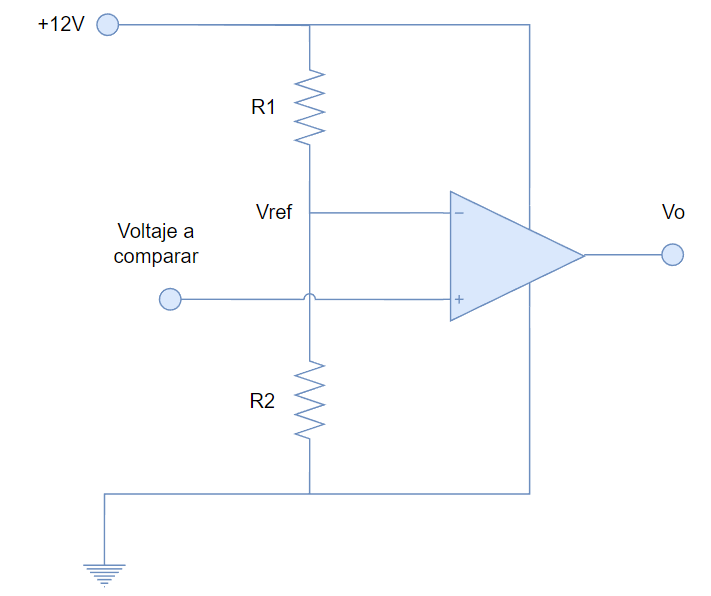
Aquí, sí podemos trabajar cómodamente con la salida saturada a uno u otro extremo, porque es así como trabaja este comparador.

De la fórmula 1, se puede deducir que la precisión de la comparación no es exacta sino que dependerá del Voltaje de offset y de la ganancia en lazo abierto del OPAMP. Como ambos parámetros son bastante buenos en los OPAMP reales, se suele considerar que el un comparador de este tipo funciona de forma perfecta en la mayoría de casos.

Para aplicaciones más exactas, se puede corregir el Offset del OPAMP, para hacer la comparación aún más precisa.

Resumiendo, el análisis en Lazo abierto puede generar los casos de salida saturada (lo más común) o no saturada (con poca estabilidad), como se muestra en el siguiente diagrama:

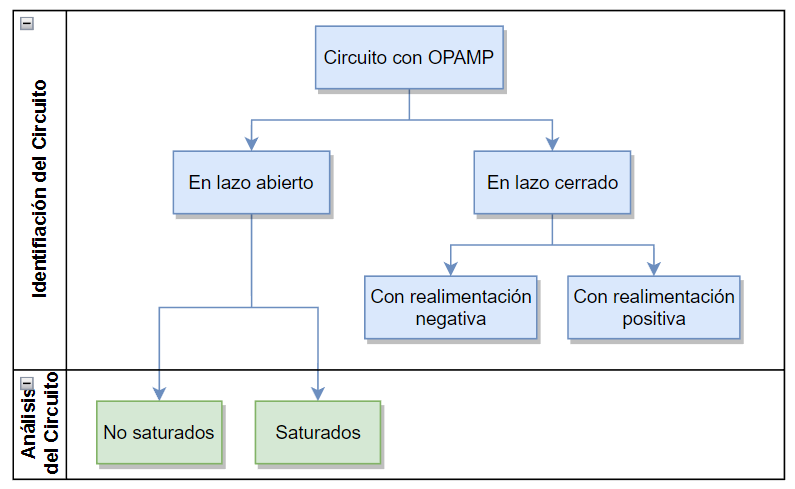
7.4 Análisis en lazo cerrado

Si bien sabemos que, el lazo cerrado en los OPAMP puede tener realimentación positiva o negativa; para esta sección supondremos que la realimentación es negativa (Ver Capítulo 3) a menos que se indique lo contrario.

Para iniciar el análisis de estos circuitos, debemos recordar que un circuito realimentado negativamente debe encontrarse en estado de equilibrio, que es lo que caracteriza a la realimentación negativa. A este estado de equilibrio, a su vez, podemos clasificarlo en dos casos:

• Circuitos no saturados (Equilibrio normal)
• Circuitos saturados (Equilibrio saturado)

Ambos son casos de estado de equilibrio pero en condiciones diferentes.

El siguiente diagrama muestra los casos de análisis vistos, tanto para los circuitos de lazo abierto como para los de lazo cerrado:

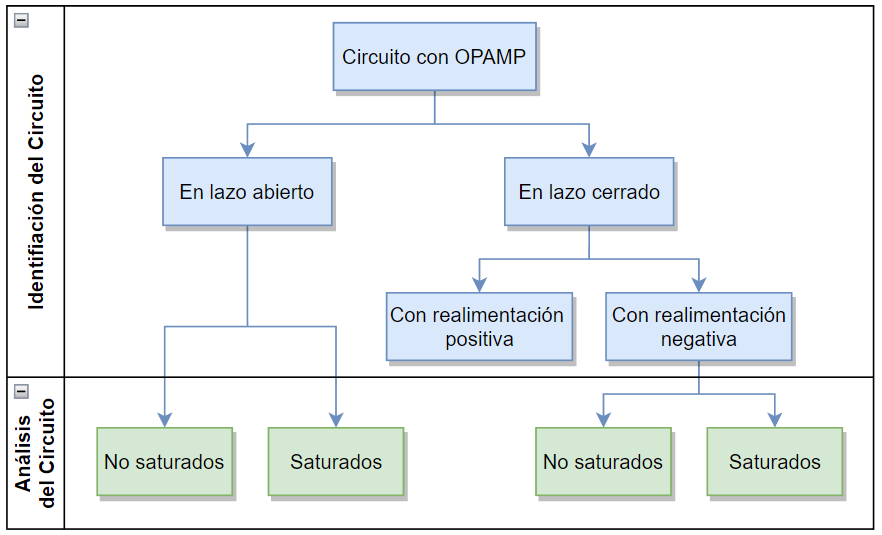
A primera instancia uno no puede decir si un circuito con OPAMP está saturado o no, salvo para casos muy obvios.

Una buena forma de realizar el análisis es:

«Hacer los cálculos, suponiendo que el circuito no está saturado, luego, cuando encontremos algún desborde en la salida, podemos concluir que estamos ante un caso de saturación.»

7.5 Ejemplo de análisis en realimentación negativa

Como ejemplo de un caso de análisis en lazo cerrado, consideremos la siguiente figura:

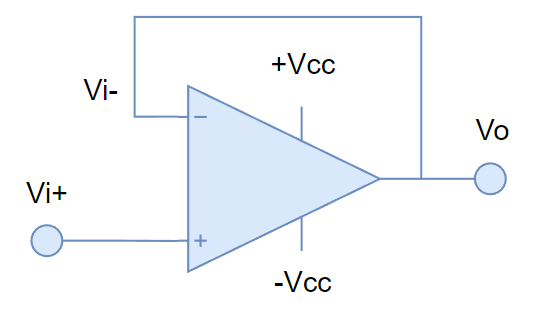
La identificación del circuito es clara, porque estamos ante un caso de realimentación negativa con un OPAMP, en su mínima expresión. Corresponde a un circuito «Seguidor de voltaje», en donde la entrada es Vi+.

La resolución aquí, se puede hacer considerando una simulación mental. Pensemos en como funciona un OPAMP, de acuerdo con la ecuación simplificada:

\begin{align}
V_o = A_d.(V_d)
\end{align} 

La fórmula simplificada (2) es completamente válida para el análisis de circuitos de lazo cerrado, salvo en casos muy particulares (En donde el voltaje de offset no sea despreciable con respecto a otros voltajes del circuito).

Esta fórmula, llevada a palabras, nos dice lo que el OPAMP «tratará» de amplificar el voltaje diferencial, sea positivo o negativo. Aquí el término «tratará» implica que no siempre se logrará esa amplificación por las limitaciones en el voltaje de salida del OPAMP.

Pero a partir de este comportamiento del OPAMP, podemos realizar una pequeña simulación mental. Imaginemos que somos el OPAMP y veamos cómo reaccionamos.

Imaginemos que por un momento el voltaje en Vi+ es más alto que Vi-. Digamos que Vi+ pasa a ser 1V, mientras Vi- estaba en 0.5V.

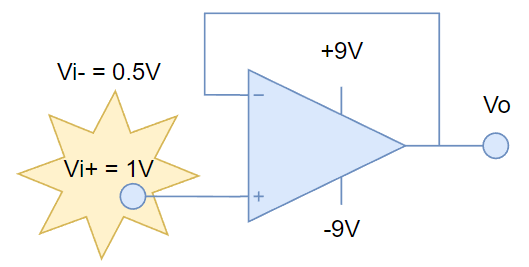
Esta condición generaría una condición de desequilibrio. Entonces nosotros, como, cualquier amplificador diferencial responsable haría, subiremos el voltaje a la salida (porque así lo dice la fórmula 2), lo que hará que en algún momento, el voltaje en Vi- alcance al valor de Vi+. En ese momento, la salida ya no subirá más y se quedará en ese estado de equilibrio, que se da justamente cuando Vo = Vi- = Vi+.

A la misma conclusión llegaremos cuando suponemos que, por un momento, el voltaje de Vi+ es menor a Vi-. De este modo concluimos que, mientras no nos salgamos del rango de trabajo del OPAMP, se cumplirá que:

V_o = V_i+

Que es la fórmula de un seguidor de voltaje.

Hasta aquí terminaría la resolución del circuito en un caso ideal. Pero si quisiéramos lidiar con un OPAMP real, deberíamos considerar también el rango de trabajo y la posible saturación.

El análisis para determinar si estamos en un caso de saturación o no, dependerá de:

• El valor exacto de Vi+.
• Los parámetros del OPAMP.

En general, mientras mantengamos a Vi+ dentro del rango permitido del OPAMP a la entrada (y haga que la salida se mantenga dentro del rango permitido del OPAMP para la salida) el seguidor no entrará en saturación ni saldrá de su modo normal de funcionamiento.

Determinar si el OPAMP entrará primero en saturación o en una zona no permitida de funcionamiento (al variar el voltaje de entrada), requeriría de un análisis más detallado de los rangos de entrada y salida del OPAMP.

Para el caso de un OPAMP «rail to rail» (a la entrada y salida) el rango de entrada del seguidor sería desde -Vcc a +Vcc. Fuera de ese rango, el OPAMP estaría fuera de su rango de funcionamiento y podría generarse saturación en la salida.

7.6 Ejercicios

EJERCICIO 1. ¿Qué nos dicen las leyes de Kirchhoff sobre los nodos y las mallas?

EJERCICIO 2. ¿Cómo se podría identificar a un circuito de lazo abierto, si solo se tiene acceso a la entrada y salida (no se conoce el diagrama)? Explique.

EJERCICIO 3. En qué se diferencia la resolución de circuitos de lazo abierto con respecto a los de lazo cerrado.

EJERCICIO 4. ¿Se podría saturar un circuito en lazo cerrado con realimentación positiva?

EJERCICIO 5. ¿Cuál es la característica principal de los circuitos con realimentación negativa? Justifique.