Introducción
Unas de las aplicaciones que más atraen visualmente, pero que más asustan a los desarrolladores, son las aplicaciones con gráficos en 3D.
Dichas aplicaciones, inicialmente estaban destinadas solo al ámbito de la ingeniería y el diseño, pero en la actualidad proliferan en diversos campos de la computación, como los juegos y la realidad virtual.
Las velocidades de los procesadores actuales, ha hecho posible que sistemas domésticos de cómputo, puedan procesar información 3D detallada y, en tiempo real, algo que hasta hace algunos años era impensable.
En el presente artículo desarrollaré una pequeña librería de funciones gráficas 3D en Object Pascal (usando Lazarus como IDE) , para dibujar sobre el lienzo, usando funciones de dibujo nativas de los sistemas operativos destino. Al estar desarrollada en Lazarus, la librería será portable a Windows, Linux y Mac.
Es claro que si lo que se quiere, es realizar procesamiento gráfico 3D, intensivo, lo mejor sería usar las herramientas de OpenGL o DirectX, pero nuestro ejemplo prescindirá de ellos, porque nuestro procesamiento 3D, será sencillo y a la vez reducimos la dependencia de librerías externas.
Resolviendo el problema
Como primer paso, debemos entender, como es que se visualiza un dibujo 3D en una pantalla plana, como la que usamos en nuestros ordenadores personales.
Una pantalla plana, jamás podrá mostrar una imagen en 3D real, por cuestiones netamente físicas. Lo que se hace es una especia de emulación 3D en un 2D, o simplemente mostrar una proyección, vista o sombra de una imagen 3D real. De esta forma, y con ayuda del cerebro, nosotros interpretamos una imagen 2D, como si de una imagen tridimensional se tratara. Añadir movimiento consistente (rotación, desplazamiento) y sombreado, ayuda al cerebro a mejorar la percepción 3D.
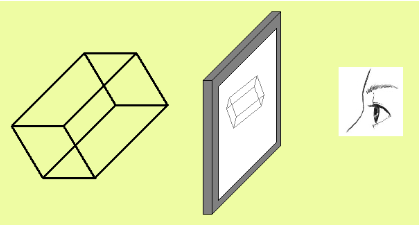
El siguiente diagrama ilustra el proceso:
Como punto de partida, y por simplicidad, usamos una imagen 3D compuesta solamente de puntos y rectas, sin considerar las superficies y las opacidades.
Como se puede ver, en la imagen, cada recta de la supuesta imagen 3D, está plenamente representada en una pantalla plana. La diferencia es que la imagen real tiene 3 coordenadas espaciales para cada punto de la recta, mientras que la imagen plana, tiene solo 2 coordenadas para cada punto de la recta. En general las rectas siguen siendo rectas, la diferencia está en las dimensiones sobre las que se mueven estas rectas (un plano o el espacio). Por ello se pueden definir a las rectas usando únicamente los puntos inicial y final.
Nuestro problema, entonces, para una transformación 3D a 2D, se reduce a trasladar un punto 3D, a un punto con 2 coordenadas. Si logramos transformar los dos puntos 3D que definen una recta, podemos entonces tener una recta en 2D, usando los dos puntos transformados.
Desde este punto de vista, lo que se necesita entonces es solamente, tener funciones de transformación 3D a 2D, y aplicarla a cada punto de la figura espacial , para luego unir los puntos mediante rectas, de forma similar a como se harían en 3D, pero en un solo plano.
Primeros pasos
Existen diversas formas de implementar una transformación 3D a 2D. Tantas como formas hay de dibujar un cubo en un papel. Algunas soluciones serán más realistas que otras, pero muchas soluciones serán percibidas como aceptables. Y en ese sentido, el cerebro humano es bastante tolerable.
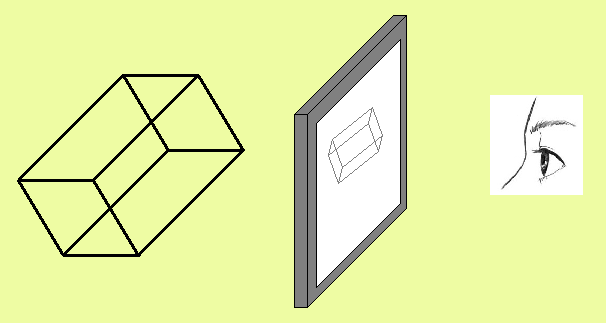
Consideremos un caso simple en coordenadas cartesianas. Nuestro mundo 3D virtual, tiene el eje Z, orientado de manera perpendicular a la línea de vista. Ahora imaginemos que queremos proyectar un punto P (idealmente seguirá siendo un punto, no importa desde que tan lejos se le mire)., a un sistema de coordenadas plano X-Y.
La transformación, en este caso, es directa, ya que la coordenada z, no tiene efecto sobre las coordenadas X e Y, simplemente afecta la profundidad o distancia del punto.
Una transformación más exacta debería considerar el efecto de alejamiento en Z, que haría que los puntos aparezcan más juntos si están más alejados. Esta transformación la realizan librerías como OpenGL, pero en nuestro caso, por simplicidad, omitiremos este efecto de alejamiento.
Imaginemos que tenemos una función en Pascal que realiza esta transformación. Su definición sería elemental:
procedure Virtual_a_Pantalla(xv, yv, zv: Double; var xp, yp: Double); begin xp := xv; yp := yv; end;
En este programa representamos, con (xv,yv, zv) a las coordenadas virtuales de un supuesto punto en 3D. Le llamaré «virtual», porque a la posición 3D que representa estas coordenadas, es ideal, no se puede representar en la computadora.
Las coordenadas (xp,yp) representan a las coordenadas de «pantalla», es decir, las que sí se pueden posicionar en el monitor de una computadora.
Nuestra función de transformación es tan elemental que solo copia las coordenadas X e Y, e ignora la coordenada Z. Por lo tanto no procesa información de profundidad. Y sin embargo, esta función de transformación es completamente válida para transformar un punto 3D en uno 2D, que se puede representar en pantalla. Si lo aplicamos a un paralelepípedo orientado en una posición especial, nos dará la imagen mostrada en el ejemplo:
Pero si el paralelepípedo se encuentra en una posición ortogonal a los ejes X,Y y Z (que es lo más usual), lo que veríamos, sería un simple rectángulo.
Como lo usual es querer ver una imagen, desde otro ángulo que no sea ortogonal, entonces lo deseable sería alguna forma de poder cambiar el ángulo de vista, o rotar cada punto de la imagen. En general ambos acercamientos son equivalentes, con ciertas excepciones.
Consideremos que vamos a rotar un ángulo ALFA a nuestro punto P, en el plano XY, y con el eje de rotación en el eje Z:
Calcular las nuevas coordenadas del punto rotado, es relativamente fácil, usando trigonometría básica. Si usamos las identidades:
alfa = alfa1-alfa2
x1 = R*cos(alfa1)
y1 = R*sen(alfa1)
x2 = R*cos(alfa2)
y2 = R*sen(alfa2)
Obtendremos:
x2 = x1*cos(alfa) + y1*sen(alfa)
y2 = y1*cos(alfa) – x1*sen(alfa)
Esto se suele expresar como una operación llamada Transformación líneal de rotación y que se expresa comúnmente, como un producto de matrices:
A la matriz de 2 por 2 se le llama matriz de rotación, que en nuestro caso es para una rotación en el plano.
Una implementación en Pascal de esta transformación sería:
procedure Virtual_a_Pantalla(xv, yv, zv: Double; var xp, yp: Double); begin xp := xv*Cos(mAlfa) - yv*Sin(mAlfa); yp := yv*Cos(mAlfa) + xv*Sin(mAlfa); end;
Aquí nuevamente estamos suponiendo que las coordenadas 3D son coordenadas virtuales y las coordenadas xp e yp, corresponden a las coordenadas a mostrar en la pantalla.
Notar que no se está usando la coordenada xv, ya que la rotación propuesta no debe verse afectada por la coordenada Z, que es perpendicular al plano visual (*).
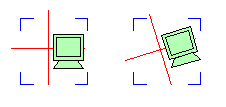
Aplicar esta operación sobre cada punto de las rectas de una imagen, nos produciría el efecto de rotación deseado:
Ahora en 3D
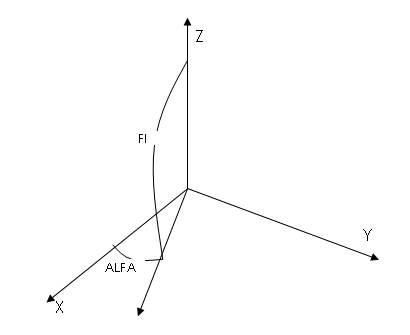
El proceso de rotación anterior es simple, ya que solo maneja un giro y no produce el efecto 3D. Consideremos, ahora un ángulo más de desplazamiento, de modo que nos permita tener una perspectiva 3D real:
Si a nuestro punto de vista, le agregamos un ángulo adicional, al que llamaremos FI, tendremos la posibilidad ahora de inclinar nuestro punto de visión, para tener una vista oblicua, del modelo 3D.
La siguiente figura muestra el efecto que tendría esta rotación adicional:
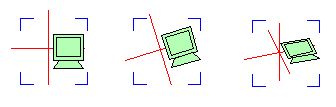 Como se puede ver, ya se puede notar el efecto 3D, a pesar de que la figura tratada, es solo una figura plana.
Como se puede ver, ya se puede notar el efecto 3D, a pesar de que la figura tratada, es solo una figura plana.
Pero ahora nuestra función de transformación varía:
procedure Virtual_a_Pantalla(xv, yv, zv: Double; var xp, yp: Double); begin xp := xv * Cos(Alfa) - yv * Sin(Alfa); yp := (yv * Cos(Alfa) + xv * Sin(Alfa)) * Cos(Fi) + zv * Sin(Fi); end;
Lo que se puede deducir de las fórmulas, es que el inclinar el ángulo de vista, solo tiene influencia en la coordenada Y. Esto mismo se puede deducir de la figura anterior: El inclinar la vista solo producirá un achatamiento vertical de la figura. Es por eso que la fórmula solo cambia en el cálculo de «yp», con una influencia rotatoria de «Fi»: cos(fi), sen(fi) .
Nuestro modelo espacial con 3 desplazamientos lineales X,Y y Z, y 2 ángulos de rotación: ALFA y FI, nos permiten generar el efecto de tridimensionalidad en una pantalla. Sin embargo, no es el único sistema para graficar en 3D, existen diversos métodos y configuraciones. Además, para que nuestro sistema espacial, sea completo, deberíamos incluir un ángulo más de rotación, de modo que tengamos 6 grados de libertad en total (3 lineales y 3 angulares), que permitirían cualquier punto de vista, para un objeto 3D.
Sin embargo, el esquema propuesto, es simple de implementar y no consume mucho procesamiento de CPU. Además nos dará algunas ventajas, ya que al permitir solo ciertos ángulos de visión, también simplifica el procesamiento de caras ocultas (si es que se implementa en este sistema de coordenadas).
En la siguiente parte, complementaremos estas fórmulas y veremos como usarlas para dibujos sencillos de puntos y rectas.
(*) En las proyecciones 3D formales, si se considera que las coordenadas X e Y de pantalla, se ven a afectadas por la profundidad, de modo que los puntos más alejados aparecen más cerca entre ellos, como se vería en una proyección en perspectiva y como lo vería una cámara común o una persona.
![]() ¿Cómo citar este artículo?
¿Cómo citar este artículo?
- En APA: Hinostroza, T. (31 de enero de 2023). Modelando al mundo – Graficos 3D en Lazarus – Parte 1. Blog de Tito. https://blogdetito.com/2023/01/31/modelando-al-mundo-graficos-3d-en-lazarus-parte-1/
- En IEEE: T. Hinostroza. (2023, enero 31). Modelando al mundo – Graficos 3D en Lazarus – Parte 1. Blog de Tito. [Online]. Available: https://blogdetito.com/2023/01/31/modelando-al-mundo-graficos-3d-en-lazarus-parte-1/
- En ICONTEC: HINOSTROZA, Tito. Modelando al mundo – Graficos 3D en Lazarus – Parte 1 [blog]. Blog de Tito. Lima Perú. 31 de enero de 2023. Disponible en: https://blogdetito.com/2023/01/31/modelando-al-mundo-graficos-3d-en-lazarus-parte-1/

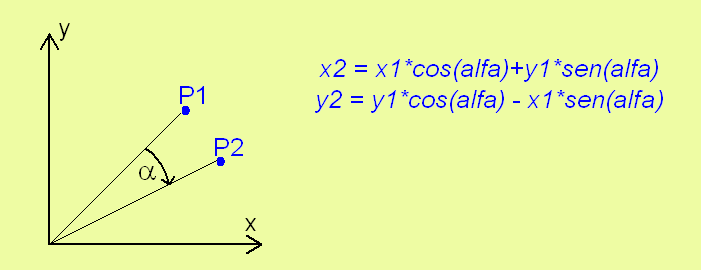
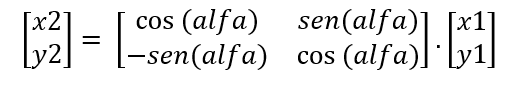
Dejar una contestacion