OPAMP – Cap. 8 – Análisis de circuitos con realimentación negativa

En el Capítulo 7 se hizo una introducción al Análisis de Circuitos con Amplificadores Operacionales, proponiendo un método de análisis y se mostró un ejemplo de resolución aplicado a circuito realimentado negativamente.

En este Capítulo se describirá, más detalladamente, la resolución de circuitos con Realimentación Negativa incluyendo los casos de circuitos saturados.

8.1 Circuitos con realimentación negativa no saturados

La característica de este tipo de circuitos es que se encuentran en un estado de equilibrio estable, que es lo que se busca en la mayoría de circuitos. En este estado de equilibrio, se cumplen ciertas características:

1. El voltaje diferencial del OPAMP es cero o muy cercano. Otra forma de expresar lo mismo sería que los voltajes de la entrada inversora y no-inversora son iguales.
2. El voltaje de salida se encuentra en el rango permitido de salida del OPAMP (No se satura).
3. El circuito compensará cualquier intento de incrementar el voltaje diferencial.

A este estado de equilibrio podríamos llamarlo también «estado lineal» o «equilibrio lineal» del circuito, sin embargo, este nombre solo aplicaría a ciertos circuitos que tienen una respuesta lineal a la salida, excluyendo a otros que, sin ser lineales, también pueden mantener una condición de equilibrio.

El análisis de este tipo de circuitos constituye el caso de análisis más común de los OPAMP, a tal punto que muchos textos solo explican este tipo de análisis.

Aunque este tipo de circuitos son conceptualmente diferentes a los de lazo abierto, el análisis se sostiene también sobre las reglas enunciadas al inicio de este Capítulo.

Para describir el método de análisis propuesto, empezaremos con el circuito clásico de amplificador inversor:

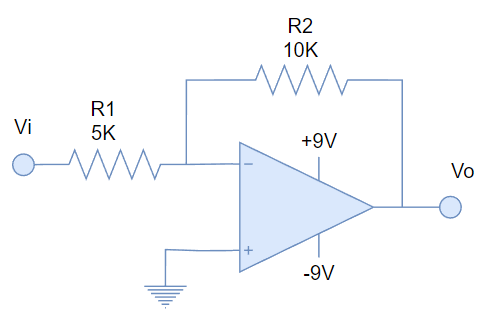
La primera pregunta que deberíamos hacernos es: ¿Qué deseamos obtener de este circuito?

En el 99% de los casos, deberemos obtener la salida como una función de entrada (función de transferencia), porque al tener esta fórmula, podemos resolver ya todo el circuito.

Esta función que, que tendrá la forma Vo = f(vi), se puede construir, usando lo que ya sabemos sobre un OPAMP y usando la función de salida simplificada que ya hemos visto:

\begin{align}
V_o = A_d.(V_d)
\end{align} 

La estrategia que vamos a usar es similar a la que se uso en la sección 7.5, considerando que el OPAMP se comportará como lo que es (Un Amplificador Diferencial de alta Impedancia).

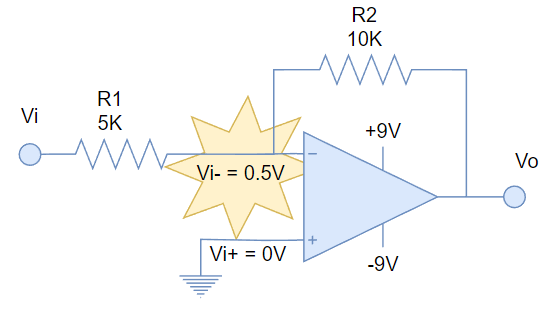
Asumimos que estamos en una posición de equilibrio, en donde Vi+ = Vi-, y tratemos de sacar al OPAMP de su zona de confort.

Como la entrada Vi+ está fijada a tierra, lo que nos queda sería mover el voltaje de Vi-. Imaginemos que por un momento muy pequeño, podemos poner un voltaje de 0.5V en la entrada Vi-.

En ese momento, el OPAMP detectará un voltaje diferencial negativo y tratará de amplificarlo fuertemente, mandando la salida a un nivel bajo de voltaje (llegando seguramente a saturación si nada se lo impide).

Pero al bajar el voltaje de salida, también estará afectando a voltaje de Vi-, originando que baje también, por efecto de R2. De esta forma. podemos decir que el OPAMP buscará la condición de equilibrio.

Aquí, la pregunta clave aquí es ¿Cuánto cambia Vi- por efecto de Vo?

Para facilidad del análisis podemos dejar solo la malla que nos interesa:

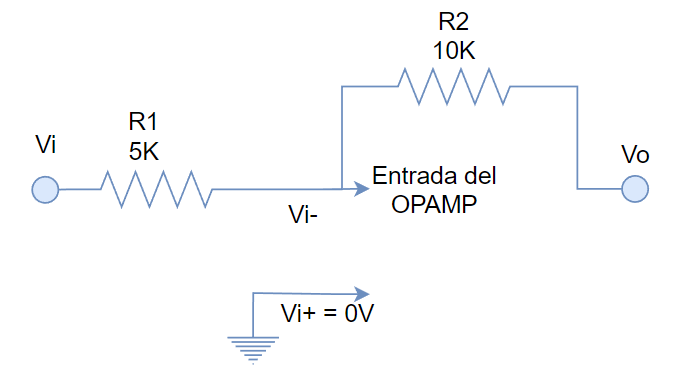
Como el OPAMP tiene alta impedancia (en comparación con R1 y R2) despreciamos la corriente que ingresa a la entrada del OPAMP.

Aquí lo que tenemos que Vi- es un voltaje intermedio entre los voltajes Vi y Vo. Hay varias formas de enfocar este problema, pero en todos los casos se llega a la misma respuesta. Personalmente, lo prefiero analizar calculando la corriente de Vo a Vi y la caída de voltaje en R2. Para eso, primero estoy asumiendo que Vo es mayor a Vi (En realidad esa suposición no importa y solo me es útil para asignar un sentido a la corriente) y, por lo tanto la corriente que va de Vo a Vi es:

I_{lazo}=\frac{Vo-Vi}{R1+R2}

Luego puedo calcular la caída de voltaje en R2:

V_{R2}=I_{lazo}.R2\\
V_{R2}=\frac{R2}{R1+R2}.(Vo-Vi) \\

Finalmente, calculo el voltaje en Vi-:

V_{i-}=V_o - V_{R2} \\
V_{i-}=V_o - \frac{R2}{R1+R2}.(V_o-V_i) \\

Como sabemos que el OPAMP buscará la condición de equilibrio, podemos asumir que lo logra poniendo Vi- = Vi+ = 0.

Bajo esa condición, podemos simplificar la ecuación anterior:

0=V_o - \frac{R2}{R1+R2}.(V_o-V_i) \\
V_o = \frac{R2}{R1+R2}.(V_o-V_i) \\
V_o.(R1+R2) = R2.V_o-R2.V_i \\
V_o.R1= -R2.V_i \\

Finalmente obtenemos la ecuación final del amplificador inversor:

\begin{align}
V_o= \frac{-R2}{R1}.V_i 
\end{align} 

Como tenemos los valores de las resistencias R1 y R2, podemos simplificar la fórmula (2), y obtenemos:

\begin{align}
V_o= \frac{-10K}{5K}.V_i  = -2V_i
\end{align} 

En realidad, se puede llegar al mismo resultado con menos cálculo, y hasta por simple observación.

SIMPLE OBSERVACIÓN

El método de simple observación consistiría en que, al ver la figura 8.1, y asumiendo que el circuito se equilibrará, se notará que para que la salida del OPAMP compense una subida de voltaje en Vi-, debe reaccionar bajando el voltaje de Vo y viceversa. Así se puede deducir que el signo de la salida debe ser opuesto al de la entrada, como se observa en la ecuación (3).

Luego, se puede también estimar el valor exacto, asumiendo que el voltaje es 0 en Vi- y que la corriente que circula por R1 es la misma que circula por R2, Por lo tanto el voltaje en Vo debe ser proporcional a Vi en el factor R2/R1. Por lo tanto, debe cumplirse:

V_o= -\frac{R2}{R1}.V_i = -2V_i

Si bien, se pueden llegar a resultados rápidos siguiendo este método algo mecánico, y varias suposiciones, no conviene pasar por alto un análisis más completo como el que hemos realizado aquí. En otras palabras: Para predecir cómo se comportará un OPAMP real, hay que saber cómo funciona un OPAMP real.
Este es solo un ejemplo de Análisis de Circuito realimentado negativamente, pero el mismo método puede seguirse para analizar a todos los circuitos realimentados negativamente, e inclusive se puede extender a circuitos realimentados positivamente, como veremos más adelante.

RANGO DE FUNCIONAMIENTO

La ecuación (3) que hemos obtenido, es válida para un caso ideal. Lo que debemos hacer ahora, si queremos aplicarlo a un OPAMP real, sería definir el rango de trabajo.

Para ello, debemos primero determinar si el amplificador se saturará primero en la entrada o la salida.

Como se trata de un Amplificador (con ganancia -2), y asumiendo que nuestro OPAMP es «rail to rail», podemos determinar que será la salida la que alcance primero los valores límites del OPAMP.

Si limitamos la salida de la ecuación (3) para que no se escape del rango de salida del OPAMP; tendremos:

-V_{cc} < V_o <+V_{cc}  \\
-9V < V_o <+9V  \\
-9V < -2V_i <+9V \\
-4.5V < -V_i <+4.5V 

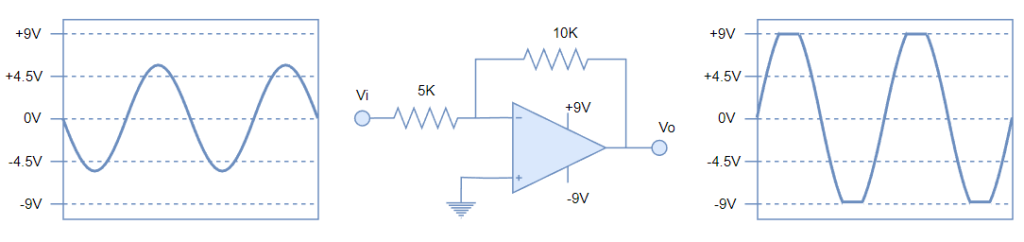
Por lo tanto, el rango permitido a la entrada del amplificador, para evitar que la salida se sature, será [-4,5V, +4.5V].

En cualquier momento en que la entrada escape de este rango, la salida dejará de ser proporcional al voltaje de entrada (pierde la linealidad).

Imaginemos que sometemos al amplificador a una señal sinusoidal de 10V pico a pico (Desde -5V a +5V). La salida será entonces recortada como se muestra en la siguiente figura:

8.2 Circuitos con realimentación negativa saturados

El estado saturado indica que el voltaje de salida ha llegado al valor máximo que permite el OPAMP (que puede ser el mayor valor positivo o el menor valor negativo, asumiendo que tiene alimentación simétrica) en busca de la condición de equilibrio.

Podemos poner como ejemplo al amplificador inversor de la sección anterior (Figura 8.1), alimentado con +-9V y con ganancia: A_v = -2.

Si ponemos 6V a su entrada, el amplificador debería generar -12V a su salida, pero como el OPAMP está limitado por la alimentación; lo más que podría generar en ese caso es -9V (Asumiendo que se usa un OPAMP de riel a riel).

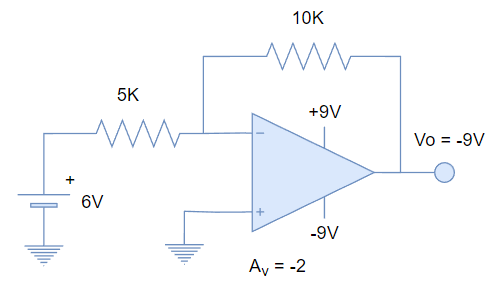
Este correspondería a un caso de circuito con OPAMP que se encuentra saturado, pero en estado de equilibrio. Se dice que está en estado de equilibrio porque el voltaje de salida se mantendrá saturado pero en un valor fijo, «esperando» a llegar a su equilibrio natural. De hecho, si la alimentación se incrementara a +-18V, el amplificador saldría de saturación, generando -12V a su salida.

8.3 Circuitos con realimentación positiva

En condiciones normales, los circuitos con realimentación positiva, incrementan aún más su ganancia, en comparación a los circuitos de lazo abierto.

Este incremento adicional en la ganancia tiene como efecto adicional el incremento de la inestabilidad del circuito y el incremento de las posibilidades de saturación.

¿Por qué se utilizaría entonces un circuito con realimentación positiva entonces? En realidad no se usan mucho y solo es común cuando queremos crear oscilación, o bloqueo de la salida (mantener el estado de saturación).

Consideremos un caso directo de realimentación positiva:

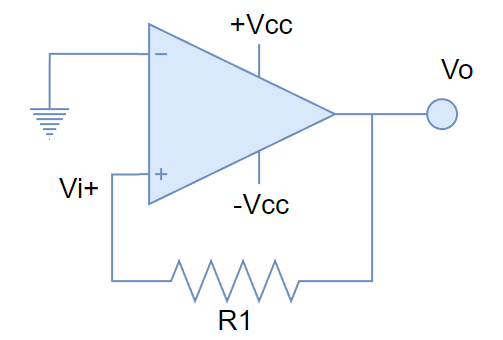
Para iniciar la resolución del circuito, podemos asumir hipotéticamente que el circuito se encuentra en equilibrio (Tal vez con Vi+ = 0V). Luego démosle un pequeño impulso, poniendo un voltaje muy pequeño en Vi+, tal vez algo de 0.1V. En ese momento el voltaje diferencial será positivo, y por la ganancia elevada del OPAMP, la salida se disparará a un valor de saturación cercano a +Vcc. Ese incremento de voltaje en la salida originará que Vi+, suba aún más, por efecto de R1, reforzando todavía más a la saturación. Por efecto de la alta impedancia de entrada del OPAMP, es seguro que Vi+ llegará a un muy cercano al valor máximo de Vo.

Esta condición de saturación constituye un estado estable (o de equilibrio saturado) y se mantendrá así, por toda la eternidad si no se desconecta antes.

Pero no es el único estado estable de este circuito, porque si bajamos el valor de Vi+ a menos de 0V, podemos deducir, por un razonamiento similar al caso anterior, que ahora la salida se saturará a -Vcc, y se mantendrá estable allí.

Este constituye un caso de circuito biestable o de dos estados estables. Funciona como una memoria electrónica que puede almacenar dos valores y mantenerlos. Este sería una aplicación de circuitos realimentados positivamente.

La condición que asumimos inicialmente Vi+ = 0V, difícilmente podría considerarse como estable por la inestabilidad de la realimentación positiva y por las imperfecciones del propio OPAMP. Así, aunque esta condición estable es casi imposible, nos ha servido bien para resolver el comportamiento del circuito.

Otra aplicación de la realimentación positiva es para la construcción de osciladores, que se describirá más adelante.

8.4 Ejercicios

EJERCICIO 1. ¿Cómo se determina que un circuito amplificador con un OPAMP se encuentra en estado saturado? Explique.

EJERCICIO 2. ¿Cuál es el voltaje de salida en el siguiente circuito?

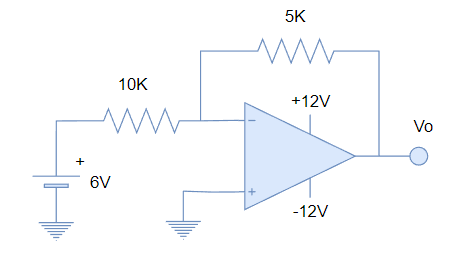
EJERCICIO 3. ¿Cuál es el voltaje de salida en el siguiente circuito?

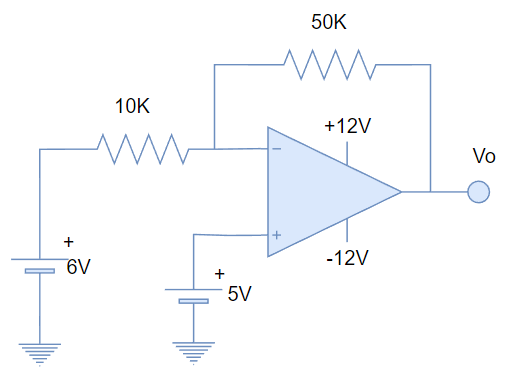
EJERCICIO 4. ¿Encontrar la ecuación que describe al siguiente circuito (Salida en función de la entrada)?

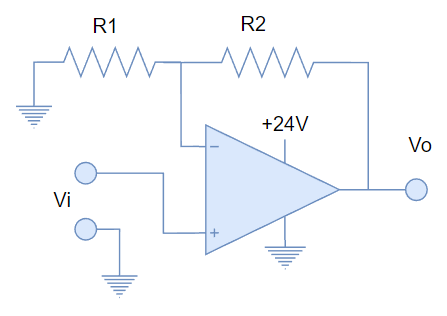
EJERCICIO 5. ¿Qué niveles de voltaje, a la entrada, saturarían al circuito del EJERCICIO 4?