Mundo Digital – Cap. 1 – Ceros y unos

1.1 Introducción

Es solo cuando la electrónica pudo proporcionarnos semiconductores confiables y de tamaño reducido, que se produjo la explosión cámbrica del mundo digital.

Atrás quedaron los circuitos de lógica cableada con interruptores, los construidos con dispositivos electromagnéticos (relés) o de tubos al vacío.

Otro gran impulso se produjo cuando el hombre abandonó su sistema de numeración decimal para pasar a uno más fácil de manejar que es el sistema binario.

En este capítulo se hará una introducción al sistema de numeración binaria y la lógica digital, desde la perspectiva de los circuitos electrónicos.

1.2 Sistema de numeración binario

Nuestras computadoras digitales hablan el lenguaje de los bits. Un bit es la unidad mínima de información y solo puede tener dos valores (que convencionalmente fijamos en 0 y 1).

En el mundo matemático un bit de información se puede representar como un dígito binario. Por eso, para entender mejor el lenguaje de los circuitos digitales, conviene repasar el sistema de numeración binario y la lógica booleana.

Así como podemos escribir nuestros números comunes en base 10 (base decimal):

0, 1, 2, 3, 99

También podemos escribir los mismos números en base 2 (base binaria):

0, 1, 10, 11, 01100011

Los números en base 2 se suelen escribir con el subíndice (2)

0₍₂₎, 01100011₍₂₎, (101)₂

Por ejemplo, una cuenta ascendente de números en binario puede ser:

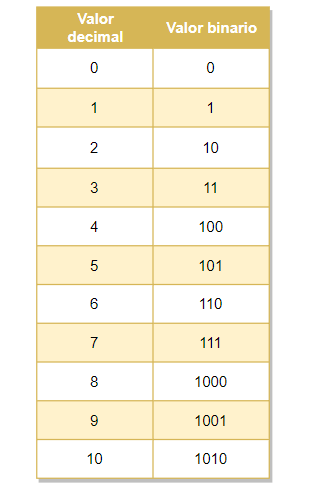
Para convertir un número en base 10 a base 2, podemos usar el método de divisiones sucesivas:

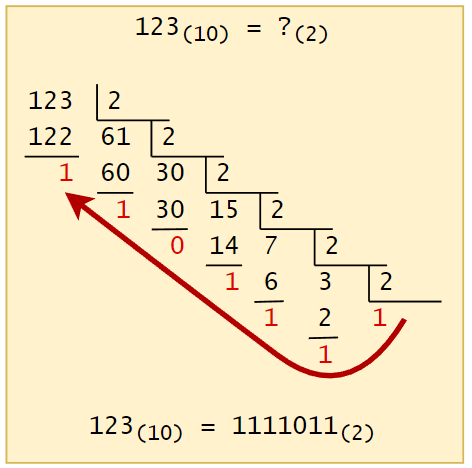
El método consiste en dividir sucesivamente el número por dos, hasta que el dividendo sea menor que dos. El número en base dos se formará tomando el último cociente obtenido y los residuos que quedaron, como se indica en la figura.

También se puede usar una calculadora o algún programa de cálculo.

La conversión de binario a decimal, se puede usar el método de acumular potencias de dos, de acuerdo a como se muestra en el siguiente diagrama:

Así como se puede trabajar en binario, también se puede trabajar en cualquier otra base.

1.3 Números binarios en electrónica digital

Al igual que en base decimal, los ceros a la izquierda no son significativos, así que da lo mismo escribir 0010 que 10

Pero en electrónica digital se acostumbra escribir los números con una cantidad de dígitos fija, inclusive si se trata de ceros a la izquierda. Esta notación sirve indicar la capacidad de almacenamiento disponible de algún dispositivo electrónico. Por ejemplo, cuando escribimos 0011₍₂₎, nos referimos al número 3 pero expresado en 4 dígitos binarios, porque podría ser que no estemos refiriendo al valor almacenado en un registro de 4 bits o al valor de alguna posición de la memoria con tamaño de 4 bits.

La cantidad de bits cuenta en electrónica, porque las computadoras manejan la memoria en paquetes o palabras de una cantidad limitada de bits. Las primeras computadoras usaban palabras de 8 bits, (1 byte), 9, 10, 12 o 14 bits. Posteriormente se usaron múltiplos de bytes: 16 bits o 32 bits. Actualmente nuestras computadoras manejan palabras de 64 bits, pero existen aún microprocesadores o microcontroladores que manejan muchos menos bits.

Con un bit podemos expresar 2 valores, con 2 bits podemos expresar 4, y así sucesivamente.

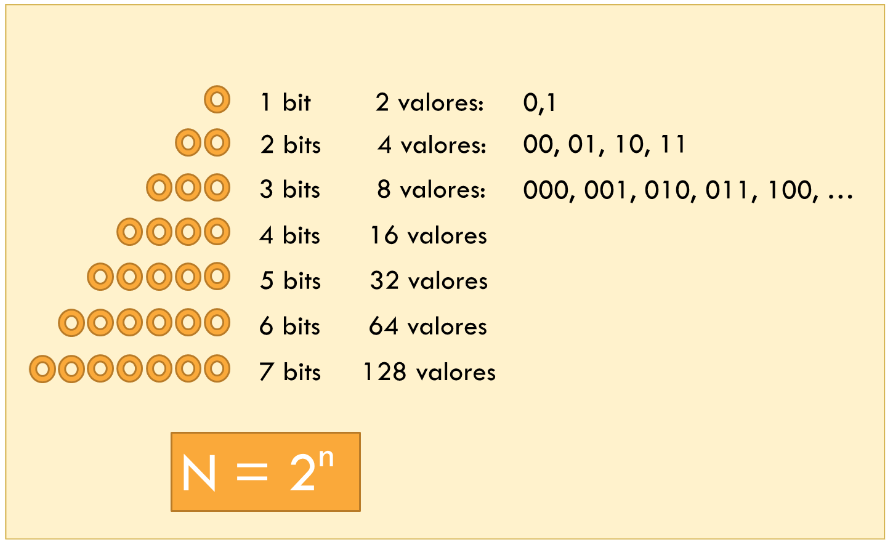
En electrónica digital y en programación, tampoco solemos escribir el subíndice 2 para los números en base 2, sino que se omite. Se prefiere usar usa algún prefijo o sufijo:

%0011, b0011, 0011b

Sin embargo, y por comodidad, no se suele expresar los números en base dos, por ser difíciles de leer y retener, sino que se prefiere usar la base 16, de modo que trabajamos mejor con números en hexadecimal.

La siguiente tabla muestra la equivalencia entre decimal binario y hexadecimal.

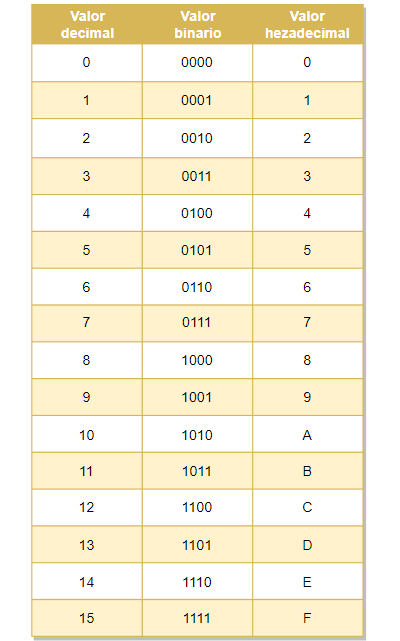
Como en hexadecimal necesitamos necesitamos 16 caracteres numéricos; se toman las primeras 6 letras del alfabeto para completara los dígitos faltantes.

Con cada dígito hexadecimal se pueden representar exactamente 4 dígitos binarios, así se simplifica considerablemente la escritura de números binarios:

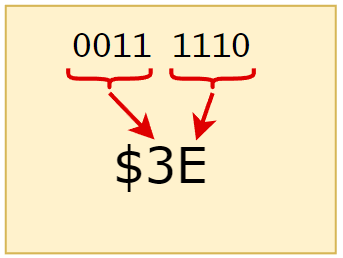
Como la transformación hexadecimal binario es directa, pues solo se trabaja en grupos de 4 bits, se prefiere el uso de números en hexadecimal en el ambiente de electrónica digital, arquitectura de computadoras y lenguajes de programación de bajo nivel.

Para identificar mejor a los números en hexadecimal se usa el prefijo «$», «0x» o el sufijo «h»:

$FFFF, 0x10, 123Ah

1.4 Los bits dentro de la computadora

Por muy complejas que parezcan ser, las computadoras solo pueden manejar ceros y unos. Pero no existe un número cero o uno dibujado en los cables de las computadoras. Tampoco hay lamparitas adentro de los chips para indicar que se ha recibido un 1 o un 0.

Los valores lógicos, en la electrónica digital, se manejan como magnitudes de voltajes altos o bajos. Los valores que representan al valor lógico 1 están cerca a 5V (o algo menos) y los valores del valor lógico o están cerca de 0V.

Como nosotros no podemos ver voltajes; no podemos ver los bits fluir por las patitas del los chips o por las pistas de los circuitos impresos. Pero, aunque pudiéramos ver voltaje (algo parecido a lo que hacen los tiburones), la velocidad con que los bits se mueven por los conductores sería tan alta que probablemente solo veríamos unos cuantos destellos.

La siguiente imagen (obtenida gracias a http://www.visual6502.org) es una animación de cómo se vería una sección del interior de la CPU 6502, en pleno funcionamiento, si pudiéramos ver los voltajes en color:

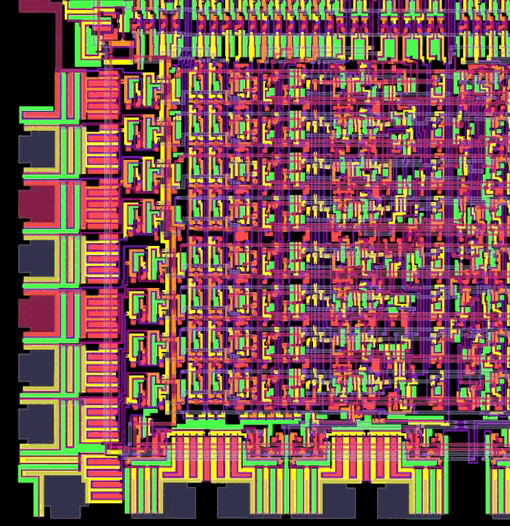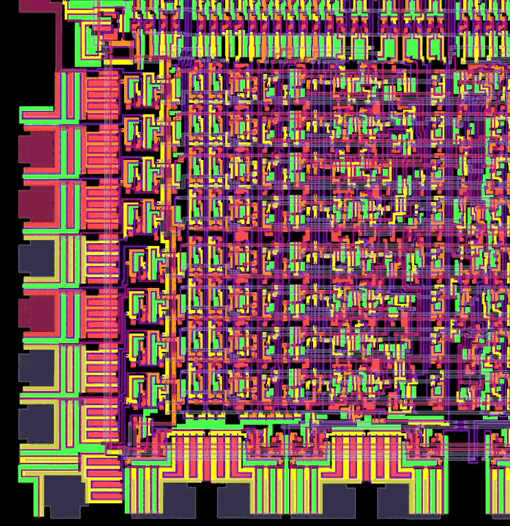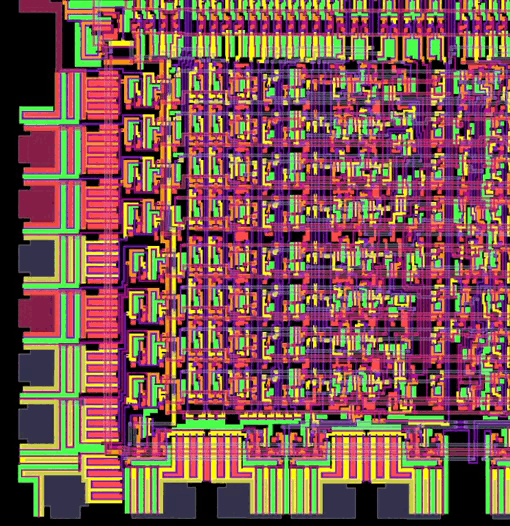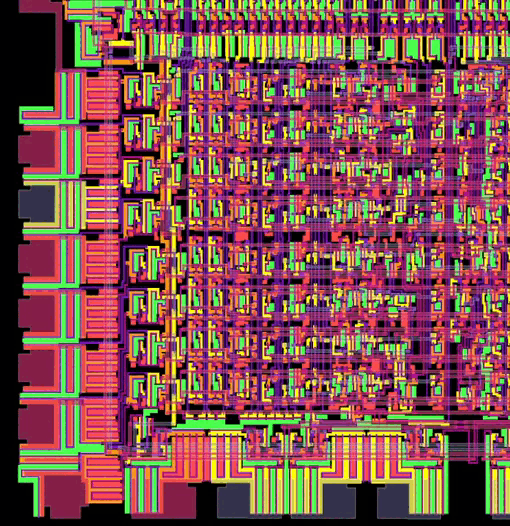
Como los bits nos resultan invisibles; tendremos que conformarnos con saber que se mueven a gran velocidad por los cables y circuitos de nuestra computadora.