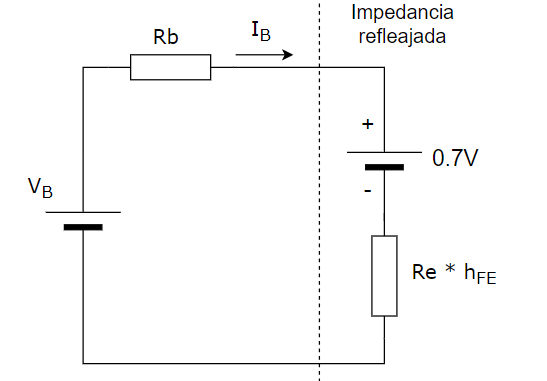
Un método bastante práctico en la solución de circuitos con transistores BJT, y que extrañamente es poco conocido y mencionado, es el método de reflexión de la impedancia del emisor en la base.
Consideremos el siguiente circuito:
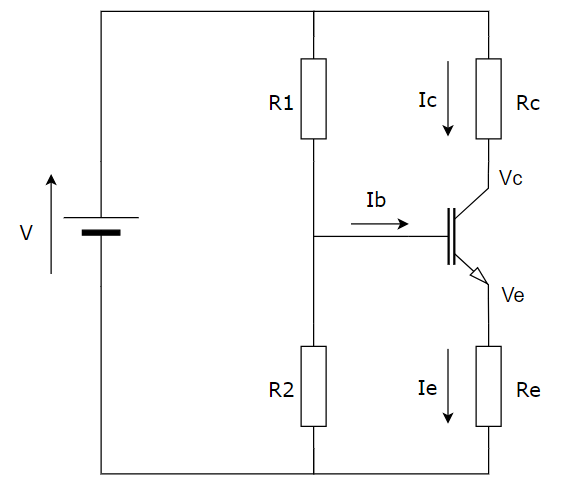
Este es el caso más general de polarización de un transistor, y que incluye a las respectivas resistencias de base, de colector y de emisor.
Una simple aplicación del teorema de Thevenin nos permite reducir el circuito a la forma:
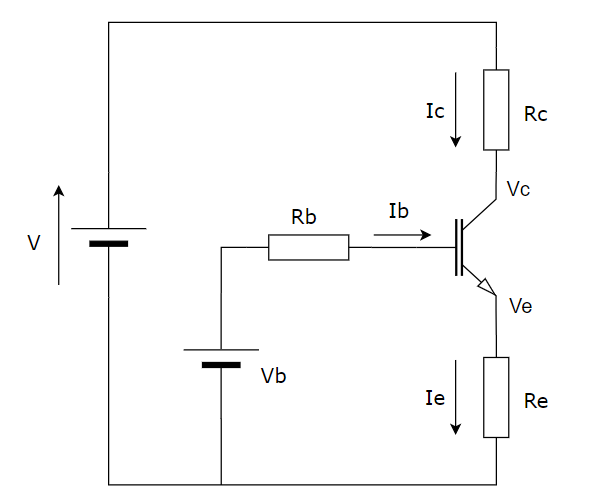
Donde:
Vb = V * R2/(R1+R2)
Rb = R1 || R2
Este sería el circuito de partida de nuestro análisis.
Veremos ahora la resolución de la corriente de base, que prácticamente resuelve todo el circuito, porque a partir de ella y con un cálculo simple podemos ver si el circuito se encuentra en corte, saturación o en región activa.
El cálculo de la corriente de base, asumirá que el transistor BJT se encuentra en la región activa. Luego, se podrá confirmar o descartar esta suposición.
Modelado del transitor
Como es común en ingeniería electrónica, se requiere usar un modelo matemático que represente a nuestro componente activo, el transitor.
Aunque existen diversos modelos propuestos, nosotros usaremos uno de los modelos más simples que nos sirve bien para realzar un análisis en DC:
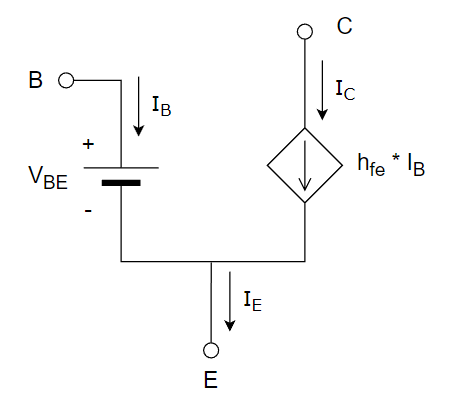
Este modelo corresponde al de un transistor BJT de tipo NPN.
En este modelo, el voltaje VBE es fijo y corresponde a 0.7 para los transistores de silicio (los más comunes), y 0.3 para los transistores de germanio.
A diferencia de modelos más elaborados, como los Eber-Molls o el modelo híbrido, este modelo aproximado es fácil de analizar y proporciona resultados bastante cercanos cuando analizamos el punto de equilibrio del circuito, cuando el transistor se encuentra en la región activa de trabajo.
Este será el modelo que usaremos para nuestro análisis siguiente.
Enfoque clásico
El circuito de la Figura 4, en donde se conocen V, Rc, Re, hFE y también los valores de VB y Rb, es la configuración simplificada que se obtiene a partir de la Figura 1.
El método clásico de solución de este problema consiste en plantear las ecuaciones de las mallas de base y del colector, considerando el modelo del BJT indicado en la Figura 3:
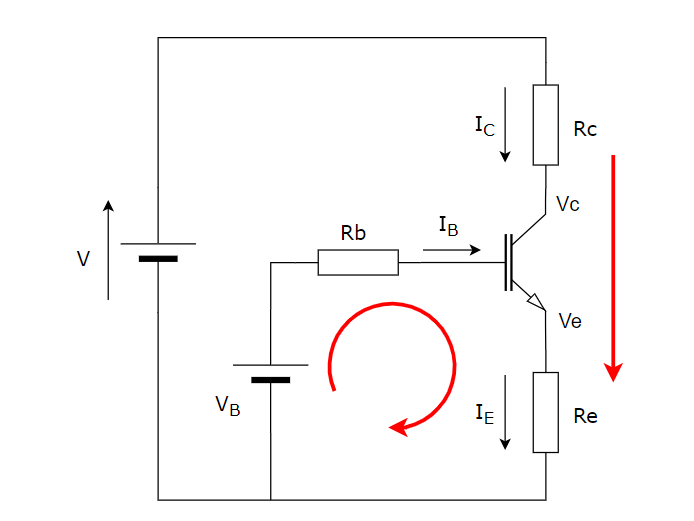
La malla de base nos da la primera ecuación:
VB – Ib*Rb – 0.7 – IE * Re = 0 …………………………………… (1)
La malla de colector nos dice:
V – IC*Rc – Vce – IE * Re = 0 …………………………………… (2)
Esta ecuación no la necesitaremos hasta el final, cuando deberemos validar el estado final del transistor (Activa, corte o saturación).
Para hallar la relación entre Ic e Ib, sabemos que:
IE = IC + IB ………………………………………………………………… (3)
Incluyendo la ganancia de corriente del transistor en (3):
IE = hFEIB + IB
IE = IB (hFE + 1)
Incluyendo esta ecuación en (1), tenemos:
VB – 0.7 = IB Rb + IB (hFE + 1) Re
De donde hallamos la forma final de IB:
IB = (VB – 0.7) / (Rb + (hFE + 1) Re ) ……………………………… (4)
Observar que si manejamos un hFE grande, como lo es en la mayoría de casos, podemos simplificar la expresión por:
IB = (VB – 0.7) / (Rb + hFE Re ) …………………………………….. (5)
Ahora, si quisiéramos continuar nuestro análisis, podemos usar este valor de IB, y la fórmula (3), en la ecuación (2) para hallar el valor de VCE y determinar si el transistor se encuentra en región activa o en saturación, lo cual no es el objetivo de este artículo, pero en resumen podemos decir que si obtenemos un VCE negativo, el transistor se encontrará en saturación. Determinar si el transistor se encuentra en corte es aún más fácil por cuanto solo queda ver si IB es mayor a cero.
Usando reflexión de impedancias
El tema principal de este artículo es mostrar el método de reflexión de impedancias para simplificar el análisis del circuito mostrado en la Figura 1.
Para empezar, partamos de la ecuación (4) o (5) y observemos que se parece bastante a la aplicación de la ley de Ohm a un circuito con una impedancia igual a: (Rb + hFE Re ).
Este detalle matemático nos permite visualizar la entrada de un transistor como una resistencia que es igual a Re multiplicada por hFE. Esto lo podemos interpretar como que Re se ve reflejada desde la base del BJT como una impedancia afectada por hFE .
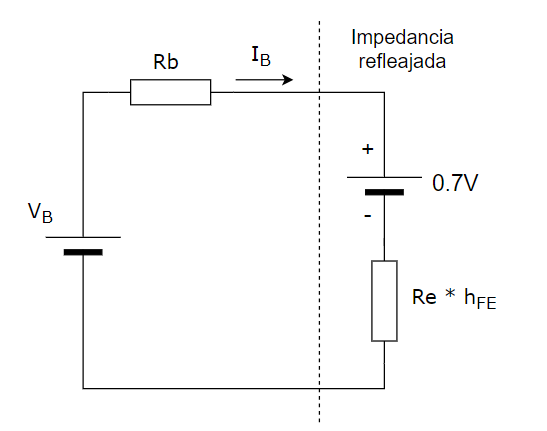
Este circuito, que es más simple de analizar a simple vista, nos lleva a la misma ecuación (5) :
IB = (VB – 0.7) / (Rb + hFE Re )
O podemos usar la forma (4) si quisiéramos ser más exactos.
Este nuevo modelo del circuito del la Figura 2 (solo la parte de la base), no solo nos permite calcular rápidamente el valor de la corriente de base, sino que, además, permite hallar, también de forma sencilla, un valor de Re par algún valor de Vb que querramos fijar.
Por ejemplo, si tenemos que nuestro VB vale 9V y Rb vale 30K, en un transistor con hFE de 100, y necesitamos poner el voltaje de la base del transistor en 6V; con un simple vistazo podemos deducir que hFE Re debe valer algo de 60K y por lo tanto; Re debe valer 600 ohmios.
Un rápido cálculo, para estos valores nos darán un valor de 6.2V para la base, lo que es un valor aproximado pero valioso si se considera que se puede calcular en pocos segundos, a partir de una simple inspección visual de la Figura 5)
Resumen
En método de reflexión de impedancias nos dice que, debido a que el transistor funciona como un amplificador de corriente, la resistencia Re del emisor, aparece multiplicada por un factor de (hfe+1) cuando «se ve» desde la base.
Este método nos permite realizar un cálculo sencillo de la corriente de base y nos sirve para resolver otros problemas referidos a la polarización del transistor BJT.
![]() ¿Cómo citar este artículo?
¿Cómo citar este artículo?
- En APA: Hinostroza, T. (15 de noviembre de 2021). Reflexión de impedancias en análisis de transistores BJT. Blog de Tito. https://blogdetito.com/2021/11/15/reflexion-de-impedancias-en-analisis-de-transistores-bjt/
- En IEEE: T. Hinostroza. (2021, noviembre 15). Reflexión de impedancias en análisis de transistores BJT. Blog de Tito. [Online]. Available: https://blogdetito.com/2021/11/15/reflexion-de-impedancias-en-analisis-de-transistores-bjt/
- En ICONTEC: HINOSTROZA, TIto. Reflexión de impedancias en análisis de transistores BJT [blog]. Blog de Tito. Lima Perú. 15 de noviembre de 2021. Disponible en: https://blogdetito.com/2021/11/15/reflexion-de-impedancias-en-analisis-de-transistores-bjt/

Excelente explicación. Simple y bien desarrollada.
Cómo se aplicaria la técnica de reflexión de impedancia en los jfet
Hola. Los JFET tienen una impedancia muy alta de entrada en comparación con los BJT, y hasta donde sé, es bastante estable, así que no tendría mucho sentido aplicar algo como reflexión de impedancias en este tipo de componentes.